题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。
要求不能创建任何新的结点，只能调整树中结点指针的指向。
注意：
需要返回双向链表最左侧的节点。
例如，输入下图中左边的二叉搜索树，则输出右边的排序双向链表。

算法1

题目要求将二叉搜索树转换为有序双向链表则采用中序遍历的方式就是输出的有序排列
整棵树采用递归的方式遍历，从根节点开始返回左子树的最左边结点，对应链表中根节点的上一个元素
右子树的最右边结点就是链表中根节点的下一个元素，以此类推，递归求解

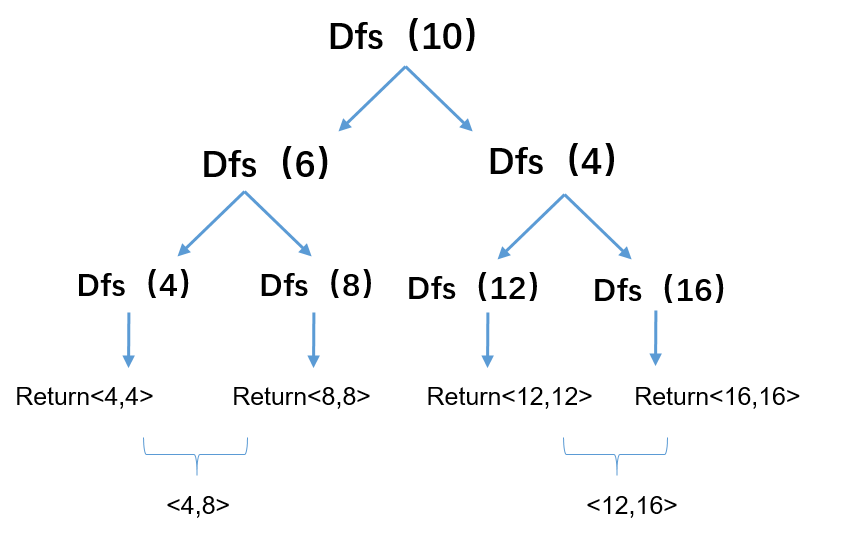
图中给出了递归过程中的程序执行流程
以及依次返回的值，一直递归调用程序。退出当前循环后继续向上一节点搜索右子树
同时采用返回pair的方式将数据组队提取出来。

C++ 代码

class Solution {

public:

TreeNode* convert(TreeNode* root) 
{
    if(!root) return root;
    auto sides = dfs(root);
    cout<<"main "<<sides.first->val<<endl;
    return sides.first;
}

pair<TreeNode*,TreeNode*> dfs(TreeNode* root){
    if(!root->left && !root->right)  return{root,root};  //递归出口 返回叶结点
    if(root->left && root->right)
    {
        auto lside= dfs(root->left);           //输出叶子结点后返回上一层循环继续执行搜索当前父结点的右孩子
        cout<<"left"<<lside.first->val<<"   "<<lside.second->val<<endl;
        auto rside=dfs(root->right);
        cout<<"right"<<rside.first->val<<"   "<<rside.second->val<<endl;

        lside.second->right=root,root->left= lside.second;
        rside.first->left = root,root->right=rside.first;
        return {lside.first,rside.second};  //返回根节点左子树的最左边结点
    }

    if(root->left){
        auto lside= dfs(root->left);
        lside.second->right=root,root->left= lside.second;
        return {lside.first,root};
    }

     if(root->right){
        auto rside= dfs(root->right);
        rside.first->left = root,root->right=rside.first;
        return {root,rside.second};

    }
}

};