题目描述

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1，某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads，其中 roads[i] = [u_i, v_i, time_i] 表示在路口 u_i 和 v_i 之间有一条需要花费 time_i 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目。由于答案可能很大，将结果对 10^9 + 7 取余 后返回。

样例

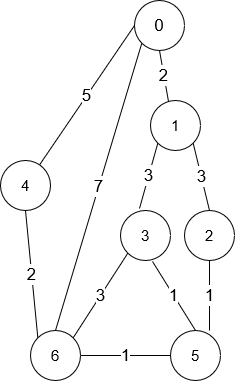
输入：
n = 7
roads = [
    [0,6,7],
    [0,1,2],
    [1,2,3],
    [1,3,3],
    [6,3,3],
    [3,5,1],
    [6,5,1],
    [2,5,1],
    [0,4,5],
    [4,6,2]
]

输出：4

解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

输入：
n = 2
roads = [[1,0,10]]

输出：1

解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

限制

• 1 <= n <= 200
• n - 1 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 3
• 0 <= u_i, v_i <= n - 1
• 1 <= time_i <= 10^9
• u_i != v_i
• 任意两个路口之间至多有一条路。
• 从任意路口出发，你能够到达其他任意路口。

算法

(最短路) $O(n^2 + m)$

1. 在求最短路的过程中顺便记录到达某个点最短路径的方案数。
2. 松弛优化时，如果发现有更优的路径，则方案数也赋值最优路径的前驱的方案数。如果发现与最优的路径长度相同，则累加当前前驱的方案数。
3. 由于图有可能非常稠密，所以采用朴素的 dijkstra 算法。
4. 注意最短路的长度可能会 超过 32 位整数的范围。

时间复杂度

• 朴素的 dijkstra 算法时间复杂度为 $O(n^2 + m)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储图以及最短路的数据结构。

C++ 代码

#define LL long long

class Solution {
public:
    int countPaths(int n, vector<vector<int>>& roads) {
        const int mod = 1000000007;
        vector<vector<pair<int, int>>> g(n);

        for (const auto &r : roads) {
            g[r[0]].emplace_back(r[1], r[2]);
            g[r[1]].emplace_back(r[0], r[2]);
        }

        vector<LL> d(n, INT64_MAX);
        vector<int> w(n, 0);
        vector<bool> v(n, false);

        d[0] = 0; w[0] = 1;
        for (int i = 0; i < n; i++) {
            LL m = INT64_MAX;
            int mi = -1;
            for (int j = 0; j < n; j++) {
                if (v[j]) continue;

                if (m > d[j]) {
                    m = d[j];
                    mi = j;
                }
            }

            v[mi] = true;
            for (const auto &e : g[mi]) {
                if (d[e.first] > d[mi] + e.second) {
                    d[e.first] = d[mi] + e.second;
                    w[e.first] = w[mi];
                } else if (d[e.first] == d[mi] + e.second) {
                    w[e.first] = (w[e.first] + w[mi]) % mod;
                }
            }
        }

        return w[n - 1];
    }
};