历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1072. 树的最长路径【树形DP】原题链接简单

作者：

一只野生彩色铅笔 , 2021-08-25 23:16:38 , 所有人可见 , 阅读 7991

160

35

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个含有 $n$ 个节点的树，以及树中每条边的权值 $w_{edge_i}$

现需要在树中找出一条路径，使得该路径上所有边的 权值之和 最大

分析

这是一道比较经典的 树形DP 题目，我们来一步步来剖析这个问题

我们知道：树上 任意两点 的路径是唯一确定的，因此我们可以暴力枚举起点和终点找出最长路径

如果这样做的话，我们来思考一下时间复杂度：

枚举起点和终点 — $O(n^2)$
找出两点之间的路径长度 — $O(\log n)$

这里找出两点之间的路径有很多种做法，预处理 st 表然后倍增求LCA、树链剖分、Link-Cut Tree

但是光是枚举起点和终点，时间复杂度 就直接拉满了，显然这种做法不可取

既然这 $O(n^2)$ 条路径不能 一一枚举，那么有什么方式可以把他们 分类枚举 呢？

我们考虑换一种 枚举方式：枚举路径的 起点和终点 $\rightarrow$ 枚举路径的 中间节点

我们先讨论一下，对于给定拓扑结构的树里的任意节点，经过他的路径有哪些：

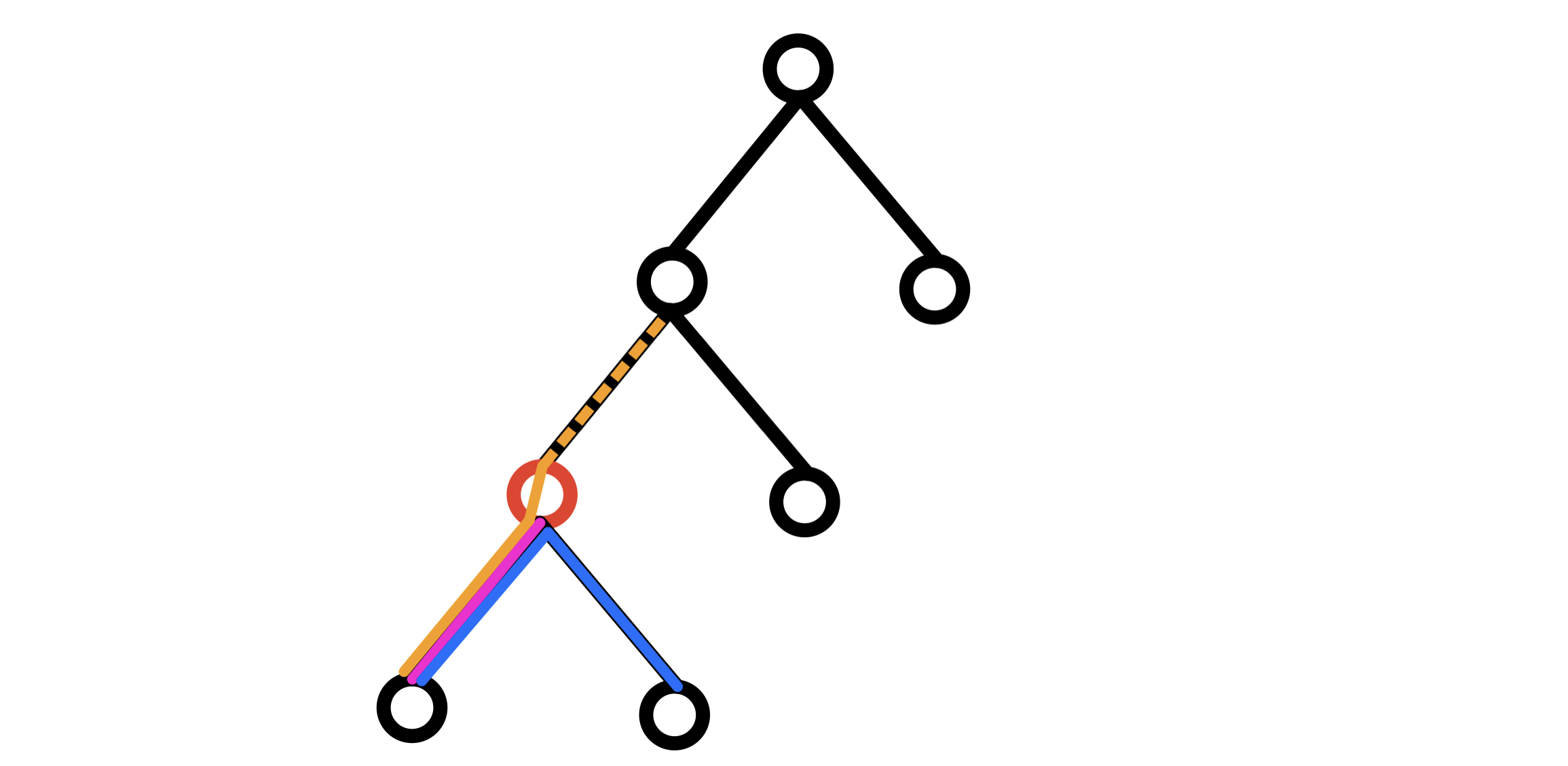
观察我标出的 红色节点，那么经过他的路径有：

以其 子树中的某个节点 作为起点，以他作为终点的 粉色路径
以其 子树中的某个节点 作为起点，以 子树中的某个节点 作为终点的 蓝色路径
以其 子树中的某个节点 作为起点，以 非其子树的节点 作为终点的 橙色路径

对于第 $1$ 种情况，我们可以直接递归处理其子树，找出到当前子树根节点最长的路径长度即可

对于第 $2$ 种情况，我们在处理第 $1$ 种情况时，顺便找出 $1$ 类路径的 次长路径

把最长和次长拼在一起，就是我们要的第 $2$ 种情况

而对于第 $3$ 种情况，我们可以把它归类为其 祖先节点 的第 $1,2$ 种情况，让其 祖先节点 去处理即可

把上述两类路径的分析，用 闫氏DP分析法 写出，就是如下形式：

闫氏DP分析法

状态表示—集合 $f_{1/2,i}$ : 以节点 $i$ 为根的子树中，从子树某个节点到 $i$ 的最长路为 $f_{1,i}$ ，次长路为 $f_{2,i}$
状态表示—属性 $f_{1/2,i}$ : 路径长度的最大值 $Max$
状态计算— $f_{1/2,i}$
$\begin{cases} f_{1,i} = max(f_{1,i_c1} + w_{i,i_{c1}}) &c1 \in i_{child}\\\ f_{2,i} = max(f_{1,i_c2} + w_{i,i_{c2}}) &c2 \in i_{child} ~\&~ c2 \ne c1 ~\&~ f_{2,i} \le f_{1,i} \end{cases}$

Code

时间复杂度： $O(n)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e4 + 10, M = N << 1; //初始不确定树的拓扑结构，因此要建立双向边

int n;
int h[N], e[M], w[M], ne[M], idx;
int f1[N], f2[N], res;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{
    f1[u] = f2[u] = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
        if (f1[j] + w[i] >= f1[u]) f2[u] = f1[u] ,f1[u] = f1[j] + w[i]; //最长路转移
        else if (f1[j] + w[i] > f2[u]) f2[u] = f1[j] + w[i];            //次长路转移
    }
    res = max(res, f1[u] + f2[u]);
}
int main()
{
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs(1, -1); //我们可以任意选取一个点作为根节点，这样整棵树的拓扑结构被唯一确定下来了
    printf("%d\n", res);
    return 0;
}

41 评论

baobaojiao 2022-11-03 11:04

我还没看y总视频呢，光看大佬的刨析就懂了👍

RwChen 2022-11-30 19:52

不建议看视频，哈哈哈

狼狗 2023-05-30 21:03 回复了 RwChen 的评论

为啥？

user.banned 2023-06-05 16:48 回复了狼狗的评论

因为彩铅佬的讲解比yxc的视频课更好。。。~~别让 $yxc$ 看到此句话~~

user.banned 2023-06-05 19:53 回复了狼狗的评论

而且 $yxc$ 要讲31分钟

九磅十六便士 2023-08-12 10:45

if (j == father) continue;什么意思

九磅十六便士 2023-08-12 15:58

顶顶顶
顶
顶顶

cxposition 2023-09-23 20:52

防止遍历重复的点，可以用st数组将father去掉，代码如下

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 7, M = N << 1;

int h[N], w[N], e[N], ne[N], idx;

int ans;

bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs(int u) {
    int dist = 0;       // dist 表示从当前这个点往下走的最大长度
    int d1 = 0, d2 = 0; // d1表示最长距离, d2表示次长距离
    st[u] = true;

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            int d = dfs(j) + w[i];
            dist = max(dist, d);

            if (d >= d1) d2 = d1, d1 = d;
            else if (d > d2) d2 = d;
        }
    }

    ans = max(ans, d1 + d2);

    return dist;
}

int main() {
    int n;
    cin >> n;

    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    dfs(1);

    cout << ans << endl;
    return 0;
}

user.banned 2023-11-12 09:02

防止重复遍历，总不能从子节点重新回到父节点吧

金陵笑笑生 2023-05-10 17:31

如果直径是负数，这个代码就过不了，然后我写了一个代码可以过负的直径，但是过不了y总的两个数据很奇怪

金陵笑笑生 2023-05-10 18:13

我想清楚了，y总的代码时，如果最长的路径是负数，那么就不要边，返回零。所以我的代码会返回负数，过不了y总的数据。

Hdw 2023-05-19 20:24 回复了金陵笑笑生的评论

明白了orz

gtt 2023-04-14 16:01

pangyou3s 12个月前

这个写法和oi-wiki上的一样hh

德布罗意の猫 2023-01-09 12:40

写的非常棒！简单易懂

WA哈哈 2022-11-18 14:54

写的真好啊

incra 2022-11-01 18:26

彩笔，你的markdown最后的公式错了，应加上{}

Makisekurisu_4 2022-02-13 23:42

彩笔的代码和变量名都十分漂亮,👍

Snow_raw 2021-11-11 23:21

非常通俗易懂，支持！！！

Hygen 2021-08-26 12:46

彩铅的iPad是什么型号的鸭

一只野生彩色铅笔 2021-08-26 17:07

我用的是18款的pro

corki 4个月前

这里不是很懂为什么第二类情况直接是最长+次长

DHT 4个月前

第二种情况即：在该节点的子树内，选经过该节点的不重复的两条边之和的最大值，所以就是最长+次长

贺杰 5个月前

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    vector<vector<int>> adj(n + 1), d(n + 1);
    vector<array<int, 2>> dp(n + 1, array<int, 2> {});
    for (int i = 1; i < n; i ++) {
        int a, b, dis;
        cin >> a >> b >> dis;
        adj[a].push_back(b), d[a].push_back(dis);
        adj[b].push_back(a), d[b].push_back(dis);
    }

    int ans = 0;
    vector<bool> st(n + 1);

    auto dfs = [&](auto self, int u) ->void {
        st[u] = true;
        for (int i = 0; i < adj[u].size(); i ++) {
            int j = adj[u][i], dis = d[u][i];
            if (st[j]) continue;
            self(self, j);
            if (dp[j][0] + dis >= dp[u][0]) dp[u][1] = dp[u][0], dp[u][0] = dp[j][0] + dis;
            else if (dp[j][0] + dis > dp[u][1]) dp[u][1] = dp[j][0] + dis;
        }
    };

    dfs(dfs, 1);

    for (int i = 1; i <= n; i ++) ans = max(ans, dp[i][0] + dp[i][1]);

    cout << ans << endl;

    return 0;
}

baikun 2024-03-02 21:43

为什么可以选任意一个点作为根节点？

秧歌star 2023-11-27 16:15

还是有不同点，y总写的少了2个数组。

风好大先生 2023-11-06 18:28

题解认准彩铅大佬

摆烂中@ 2023-07-14 12:01

h[u]是啥意思啊？？？

cocoshe 2023-05-16 01:29

dfs用一个全局的dist变量来做为啥不行捏？还有为什么是用father而不是用一个bool st[N]来记录这个点有没有被选过呢？（类似于图的遍历）orz

void dfs (int u, int fa) {
    for (int i = h[u];~i;i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        dist += w[i];
        dfs (j, u);
        if (dist >= f1[u]) f2[u] = f1[u], f1[u] = dist;
        else if (dist >= f2[u]) f2[u] = dist;
        dist -= w[i];
        // if (f1[j] + w[i] > f1[u]) f2[u] = f1[u],f1[u] = f1[j] + w[i];
        // else if (f1[j] + w[i] > f2[u]) f2[u] = f1[j] + w[i];
    }
    res = max (res,f1[u] + f2[u]);
}

xxxxiu 2023-05-23 19:48

f1[u]指的是以u为根节点的子树, 从子树的某个结点到u的最长路, 但是这份代码中, 递归到子树的话, dist带着其父节点的距离

xxxxiu 2023-05-23 19:48

可以用st数组啊

int dfs(int u)
{
    int d1 = 0, d2 = 0;
    st[u] = true;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (st[j]) continue;
        int d = dfs(j) + w[i];
        if (d >= d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
    }

    ans = max(ans, d1 + d2);
    return d1;
}

这份代码是可以过的诶

UniqueDay 2023-03-24 11:50

讲得好啊

旦驳 2023-03-19 20:30

这个题解棒，比视频清晰！！

App 内打开

AcWing 1072. 树的最长路径【树形DP】 原题链接 简单

题目描述

分析

闫氏DP分析法

Code

41 评论

AcWing 1072. 树的最长路径【树形DP】原题链接简单