部分内容摘自 各佬的博客、$Oi - Wiki$ 、y总的板书 集大成

Link - Cut Tree

LCT 是用于解决 动态树问题 的数据结构

动态树问题：

• 维护一个森林，支持删除某条边，加入某条边，并保证加边，删边后仍是!!森林!!。我们要维护该森林的一些信息。
• 一般的操作有两点连通性， 两点路径权值和， 连接两点 和 切断某条边、修改信息 等

他和 树剖 有几分相似，树剖 是通过按 子树大小 进行剖分，然后动态维护剖分出的 $\log n$ 个区间

LCT 则是用多个 Splay 来维护 多个实链，Splay 的特性就使得我们可以进行 树的合并、分割 操作

LCT 的好处在于：

1. 树链剖分 能做的 LCT 基本都能做
2. 树链剖分 处理一次询问的时间复杂度为 $O(\log^2n)$，而 $LCT$ 是 $O(\log n)$

不过需要注意，$LCT$ 的常数很大（从他的复杂性也能看出）
因此板子里可以适当增加 宏定义 和 内敛函数 （我的常数很大，评测姬你忍一下）

实链剖分

• 对于一个点连向它所有儿子的边 , 我们自己选择 一条边 进行剖分，我们称被选择的边为 实边，其他边则为 虚边。
• 对于 实边，我们称它所连接的儿子为 实儿子。
• 对于一条由 实边 组成的 链，我们同样称之为 实链。
• 对于 每条 实链，我们 分别 建一个 Splay 来维护整个 链区间 的信息。
• 正是因为 实链 我们可以自己任意选择，使得 实链剖分 可以适用于动态树的问题

惯例贴出 y总的抽象图示

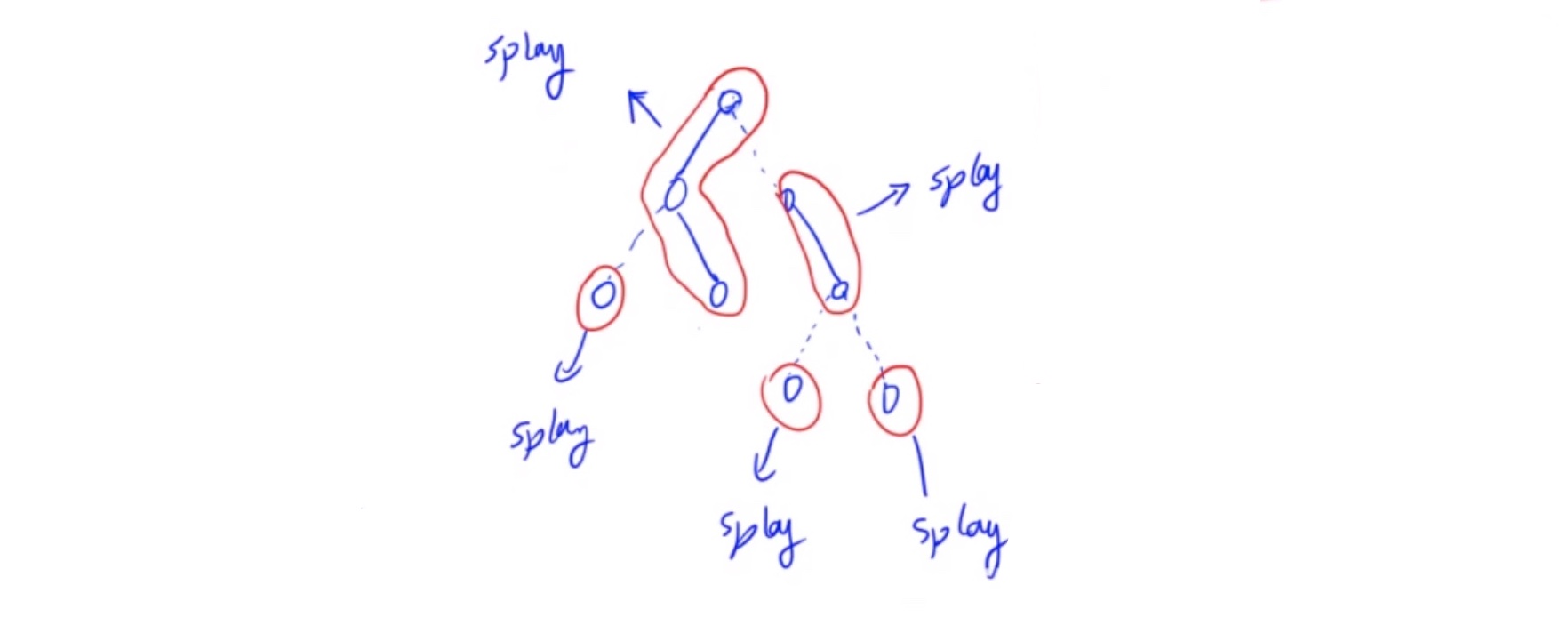
辅助树splay

• 辅助树 由多棵 Splay 组成，每棵 Splay 维护原树中的 一条路径，且 中序遍历 这棵 Splay 得到的点序列，从前到后对应原树“从上到下”的一条路径

• 原树 每个节点与 辅助树 的 Splay 节点一一对应

• 辅助树 的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点本应是空，但在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中 这条链 的父亲节点（即链最顶端的点的父亲节点）。这类父亲链接与通常 Splay 的父亲链接区别在于儿子认父亲，而父亲不认儿子，对应原树的一条 虚边。因此，每个连通块恰好有一个点的父亲节点为空。

  具体图示如下（来源：OI-WiKi）

  原树：

  

  对应辅助树：

  

辅助树和原树的关系

• 原树 中的 实链 在 辅助树 中都在同一颗 Splay 里
• 原树 中的 虚链 : 在 辅助树 中，子节点 所在 Splay 的 Father 指向 父节点，但是 父节点 的 两个儿子 都不指向 子节点。
• 原树的 Father 指向不等于 辅助树的 Father 指向。
• 辅助树 是可以在满足 辅助树、Splay 的性质下任意换根的。
• 虚实链变换 可以轻松在 辅助树 上完成，这也就是实现了 动态维护树链剖分。

以上就是对 LCT 的大致介绍，接下来只需实现 亿点点 功能函数，就完成LCT啦

Splay 系函数的变化

pushup(x)：本题需要维护的是路径的异或和

void pushup(int x)
{
    tr[x].sum = tr[tr[x].s[0]].sum ^ tr[x].v ^ tr[tr[x].s[1]].sum;
}

pushdown(x)：不同于翻转区间那题，这里懒标记维护的是 修改后 的懒标记

void pushdown(int x)
{
    if (tr[x].rev)
    {
        pushrev(tr[x].s[0]), pushrev(tr[x].s[1]);
        tr[x].rev = 0;
    }
}

rotate(int x)：在修改 z 与 y 这条边的时候特判 y 是否为根节点

在前面已经介绍过了，原本 splay 的根节点应该是没有父节点的，但 LCT 里我们让这个空指针来维护虚边

isroot(x) 函数后面会介绍

void rotate(int x)
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x; //唯一不同的地方
    tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

splay(int x)：把节点 x 转到辅助树 splay 的根节点

我先说一下这里不同的地方，以往 splay 找某个节点的时候，都是从根节点往下找（按照 BST 的性质）

但是在 LCT 中，splay 充当的是辅助树的角色，我们获得 splay 中的节点是通过原树中对应节点的编号

换而言之，我们是直接获得 splay 中的某个节点，而不是自上而下递归找到的

所以，在做 splay 转到根节点的旋转操作时，我们需要先 自上而下 把 懒标记 下传

这就是与传统 splay 相矛盾的地方

这里有两种写法，一个是递归（码量少，但是比较看评测姬心情），一个是迭代（y总的栈写法）

//递归写法
void update(int x)
{
    if (!isroot(x)) update(tr[x].p);
    pushdown(x);
}
void splay(int x)
{
    update(x);
    while (!isroot(x))
    {
        int y = tr[x].p, z = tr[y].p;
        if (!isroot(y))
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
}

//----------分割线-------------

//迭代写法
void splay(int x)
{
    int top = 0, r = x;
    stk[ ++ top] = r;
    while (!isroot(r)) stk[ ++ top] = r = tr[r].p;
    while (top) pushdown(stk[top -- ]);
    while (!isroot(x))
    {
        int y = tr[x].p, z = tr[y].p;
        if (!isroot(y))
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
}

新操作

access(x) ：建立一条从根节点到 x 的实链（同时将 x 变成对应 splay 的根节点）

1. 把当前节点转到根。
2. 把儿子换成之前的节点。
3. 更新当前点的信息。
4. 把当前点换成当前点的父亲，继续操作。

void access(int x)  //建立一条从根节点到 x 的实链（同时将 x 变成对应 splay 的根节点）
{
    int z = x;  //记录初始的节点编号
    for (int y = 0; x; y = x, x = tr[x].p) //x沿着虚边往上找根
    {
        splay(x);   //先转到当前辅助树的根
        tr[x].s[1] = y, pushup(x);  //把上个树接到中序遍历后面
    }
    splay(z);   //把初始的节点转到根
}

makeroot(x) 将 x 变成原树的根节点

access(x) 操作之后，x 会被旋转到splay的树根，此时我们只需反转 x，就可以达到反转 splay 中序遍历的效果

而 splay 中序遍历被反转，也就意味着原树中，从根节点到 x 的路径被反转，从而实现把 x 变成根的操作

void makeroot(int x) //将 x 变成原树的根节点（且左子树为空）
{
    access(x);  //此时x为辅助树的根节点，直接反转中序遍历即可
    pushrev(x);
}

findroot(x) ：找到 x 所在的原树的根节点，再将原树的根节点旋转到辅助树的根节点

先 access(x) 打通从根节点到 x 的实链（此时 x 在 splay 的根节点），然后找到该 splay 中序遍历的第一个节点

int findroot(int x) //找到 x 所在的原树的根节点，再将原树的根节点旋转到辅助树的根节点
{
    access(x);  //打通根节点到 x 的实链，当前 x 位于辅助树的根节点位置
    while (tr[x].s[0]) pushdown(x), x = tr[x].s[0];  //找到辅助树中序遍历的第一个元素（左下角）
    splay(x);   //转到根节点
    return x;
}

split(x, y) ：将 x 到 y 的路径变为实边路径

比较简单，先把 x 放到根，再打通从 根 到 y 的路径即可

void split(int x, int y)    //将 x 到 y 的路径变为实边路径
{
    makeroot(x);    //先把 x 设为根
    access(y);      //在打通根到 y 的实链即可
}

link(x, y) ：若 x , y 不连通，则加入 (x, y) 这条边

先把 x 放到根，查找一下 y 所在树的根节点是不是 x。

如果不是（查找根节点会把 y 转到他辅助树的根节点）则加边

void link(int x, int y) //若 x , y 不连通，则加入 (x, y) 这条边
{
    makeroot(x);    //先把 x 设为根
    if (findroot(y) != x) tr[x].p = y;  //如果不连通，则把 x 的实链接到 y 上即可
}

cut(x, y) ：若边 (x, y) 存在，则删掉（x, y）这条边

先把 x 放到根，判断此时：

1. y 所在的原树中的根是否是 x
2. y 的父节点是否是根 x
3. y 是否有左孩子（中序遍历紧挨在 x 的后面）

满足上述三条，说明 边 (x,y) 存在，cut 掉

void cut(int x, int y)  //若边 (x, y) 存在，则删掉（x, y）这条边
{
    makeroot(x);
    if (findroot(y) == x && tr[x].s[1] == y && !tr[y].s[0])
    {
        tr[x].s[1] = tr[y].p = 0;
        pushup(x);
    }
}

isroot(x) ：判断 x 是否是所在辅助树 splay 的根节点

这个比较简单，按照我们之前所说的，他有父亲，但他父亲不认他 泪目

bool isroot(int u)  //判断 u 是否为实链的顶部
{
    return tr[tr[u].p].s[0] != u && tr[tr[u].p].s[1] != u;
}

一些提醒（From OI-Wiki）

• 干点啥前一定要想一想需不需要 PushUp 或者 PushDown, LCT 由于特别灵活的原因，少 Pushdown 或者 Pushup 一次就可能把修改改到不该改的点上！
• LCT 的 Rotate 和 Splay 的不太一样，if (z) 一定要放在前面。
• LCT 的 Splay 操作就是旋转到根，没有旋转到谁儿子的操作，因为不需要。

Code

以下为本题完整代码：

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
struct Splay
{
    int s[2], p, v;
    int sum, rev;
}tr[N];

bool isroot(int u)  //判断 u 是否为实链的顶部
{
    return tr[tr[u].p].s[0] != u && tr[tr[u].p].s[1] != u;
}
//------------------Splay系函数------------------\\

void pushup(int u)
{
    tr[u].sum = tr[tr[u].s[0]].sum ^ tr[u].v ^ tr[tr[u].s[1]].sum;
}
void pushrev(int u)
{
    swap(tr[u].s[0], tr[u].s[1]);
    tr[u].rev ^= 1;
}
void pushdown(int u)
{
    if (tr[u].rev)
    {
        pushrev(tr[u].s[0]);
        pushrev(tr[u].s[1]);
        tr[u].rev = 0;
    }
}
void rotate(int x)
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x; //唯一的不同处
    tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}
void splay(int x)   //迭代写法
{
    static int stk[N];  //先自上而下下传懒标记
    int tt = 0, t = x;
    stk[ ++ tt] = t;
    while (!isroot(t)) stk[ ++ tt] = t = tr[t].p;
    while (tt) pushdown(stk[tt -- ]);
    //接下来基本与splay板子相同
    while (!isroot(x))
    {
        int y = tr[x].p, z = tr[y].p;
        if (!isroot(y))
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        rotate(x);
    }
}
//------------------Splay系函数------------------\\

void access(int x)  //建立一条从根节点到 x 的实链（同时将 x 变成对应 splay 的根节点）
{
    int z = x;  //记录初始的节点编号
    for (int y = 0; x; y = x, x = tr[x].p) //x沿着虚边往上找根
    {
        splay(x);   //先转到当前辅助树的根
        tr[x].s[1] = y, pushup(x);  //把上个树接到中序遍历后面
    }
    splay(z);   //把初始的节点转到根
}
void makeroot(int x) //将 x 变成原树的根节点（且左子树为空）
{
    access(x);  //此时x为辅助树的根节点，直接反转中序遍历即可
    pushrev(x);
}
int findroot(int x) //找到 x 所在的原树的根节点，再将原树的根节点旋转到辅助树的根节点
{
    access(x);  //打通根节点到 x 的实链，当前 x 位于辅助树的根节点位置
    while (tr[x].s[0]) pushdown(x), x = tr[x].s[0];  //找到辅助树中序遍历的第一个元素（左下角）
    splay(x);   //转到根节点
    return x;
}
void split(int x, int y)    //将 x 到 y 的路径变为实边路径
{
    makeroot(x);    //先把 x 设为根
    access(y);      //在打通根到 y 的实链即可
}
void link(int x, int y) //若 x , y 不连通，则加入 (x, y) 这条边
{
    makeroot(x);    //先把 x 设为根
    if (findroot(y) != x) tr[x].p = y;  //如果不连通，则把 x 的实链接到 y 上即可
}
void cut(int x, int y)  //若边 (x, y) 存在，则删掉（x, y）这条边
{
    makeroot(x);
    if (findroot(y) == x && tr[x].s[1] == y && !tr[y].s[0])
    {
        tr[y].p = tr[x].s[1] = 0;
        pushup(x);
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &tr[i].v);
    while (m -- )
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);
        if (t == 0)
        {
            split(x, y);
            printf("%d\n", tr[y].sum);
        }
        else if (t == 1) link(x, y);
        else if (t == 2) cut(x, y);
        else
        {
            splay(x);
            tr[x].v = y;
            pushup(x);
        }
    }
    return 0;
}