算法提高课汇总

算法思路

数字三角形模型, 可以用dp求解. 下面用Y氏DP–从集合的角度思考动态规划求解.

状态表示/集合定义 : dp[ i ][ j ]

• 集合 : 从起点(1,1)到(i,j)的所有合法路线

• 属性 : Max. 所有路线上花生🥜总数的最大值.

此时问题转化为求解dp[R][C].

状态计算/集合划分

• 集合划分原则 : 不重复; 不遗漏. 其中对属性为Max/Min的状态不重复不是计算时的必要条件.

• 集合划分依据 :
  $\;\; $”最后一步” / 将集合划分为若干个可以1步转移至dp[i][j]的已计算的状态

• 集合划分过程 :
  $\;\;$由状态定义出发, dp[i][j]表示 : $(1,1)$ --> $\cdots$ --> $(i, j)$, 根据题意有两种可能 :
  $\;\;\;\;$ $(1,1)$ --> $\cdots$ --> $(i-1, j)$ --> $(i, j)$
  $\;\;\;\;$ $(1,1)$ --> $\cdots$ --> $(i, j - 1)$ --> $(i, j)$

为了保证状态的Max属性, 因为从$(i-1, j)$ --> $(i, j)$或$(i, j - 1)$ --> $(i, j)$的花生数目
固定; 可变的部分是前面的路径, 回到我们状态的定义, 对应的花生数为dp[i-1][j]和dp[i][j-1].

如果用椭圆表示状态dp[i][j]对应集合 :

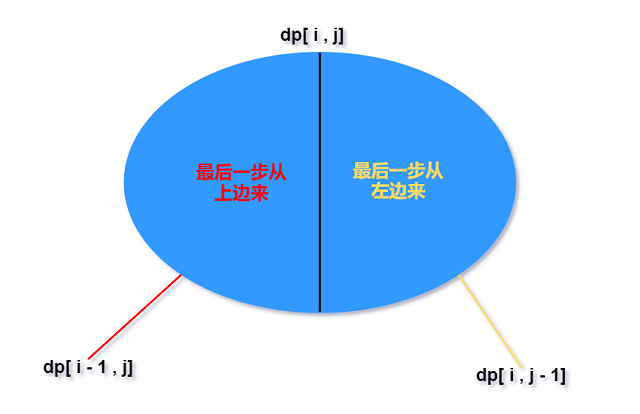
所以$dp[i][j] = max(dp[i-1][j], dp[i][j -1]) + w[i][j]$. 按照一定的顺序保证计算(i,j)时其
依赖的状态已经计算完毕.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int w[N][N];
int dp[N][N];

int main()
{
    int T;
    cin >> T;
    while( T -- )
    {
        cin >> n >> m;
        for( int i = 1; i <= n; i ++ )
            for( int j = 1; j <= m; j ++ )
                cin >> w[i][j];

        for( int i = 1; i <= n; i ++ )
            for( int j = 1; j <= m; j ++ )
                dp[i][j] = max( dp[i-1][j], dp[i][j-1] ) + w[i][j];

        cout << dp[n][m] << endl;
    }
    return 0;
}