算法分析
1、问题：为什么Dijkstra不能使用在含负权的图中？（在强大的网友指点下已进行修改）
（这是以前错误的分析，若看完这个例子分析觉得正确的说明对最短路理解得还不够透彻，这里不做删除）
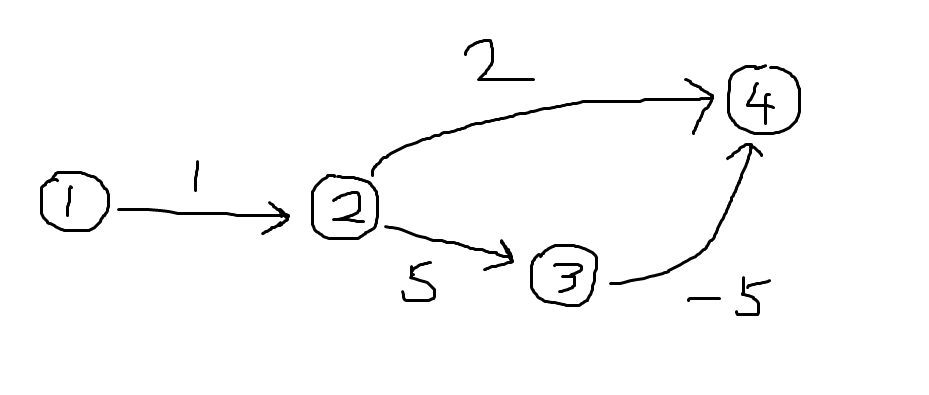
分析：如图所示：
$\quad$$\quad$若通过Dijkstra算法可以求出从1号点到达4号点所需的步数为3 (每次选择离源点最短距离的点更新其他点)
但实际上从 1 号点到达 4 号点所需步数为 1 (1 –> 2 –> 3),因此不能使用 Dijkstra 解决含负权图的问题
正确的分析
Dijkstra算法的3个步骤
- 1、找到当前未标识的且离源点最近的点
t - 2、对
t号点点进行标识 - 3、用
t号点更新其他点的距离
反例
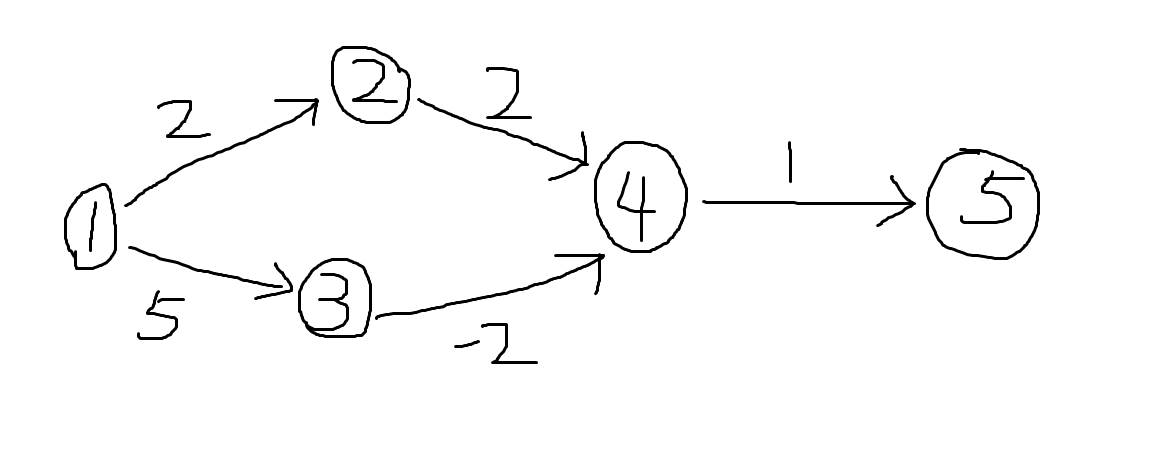
结果：
$\quad$$\quad$dijkstra算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5，算出 1 号点到 5 号点的最短距离是2 + 2 + 1 = 5，然而还存在一条路径是1 -> 3 -> 4 -> 5，该路径的长度是5 + (-2) + 1 = 4，因此 dijkstra 算法失效
dijkstra详细步骤
- 初始
dist[1] = 0 - 找到了未标识且离源点
1最近的结点1，标记1号点，用1号点更新其他所有点的距离，2号点被更新成dist[2] = 2，3号点被更新成dist[3] = 5 - 找到了未标识且离源点
1最近的结点2，标识2号点，用2号点更新其他所有点的距离，4号点被更新成dist[4] = 4 - 找到了未标识且离源点
1最近的结点4，标识4号点，用4号点更新其他所有点的距离，5号点被更新成dist[5] = 5 - 找到了未标识且离源点
1最近的结点3，标识3号点，用3号点更新其他所有点的距离，4号点被更新成dist[4] = 3 - 结束
- 得到
1号点到5号点的最短距离是5，对应的路径是1 -> 2 -> 4 -> 5，并不是真正的最短距离
2、什么是bellman - ford算法？
$\quad$Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。
$\quad$(通俗的来讲就是：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新)
3、bellman - ford算法的具体步骤
for n次
$\quad$for 所有边 a,b,w (松弛操作)
$\quad$$\quad$dist[b] = min(dist[b],back[a] + w)
注意：back[] 数组是上一次迭代后 dist[] 数组的备份，由于是每个点同时向外出发，因此需要对 dist[] 数组进行备份，若不进行备份会因此发生串联效应，影响到下一个点
4、在下面代码中，是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断，而并非是if(dist[n] == INF)判断，原因是INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可
5、bellman - ford算法擅长解决有边数限制的最短路问题
时间复杂度 $O(nm)$
其中n为点数，m为边数
Java 代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
static int N = 510;
static int M = 100010;
static int n;//总点数
static int m;//总边数
static int k;//最多经过k条边
static int[] dist = new int[N];//从1到点到n号点的距离
static Node[] list = new Node[M];//结构体
static int INF = 0x3f3f3f3f;
static int[] back = new int[N];//备份dist数组
public static void bellman_ford()
{
Arrays.fill(dist, INF);
dist[1] = 0;
for(int i = 0;i < k;i++)
{
back = Arrays.copyOf(dist, n + 1);//由于是从1开始存到n
for(int j = 0;j < m;j++)
{
Node node = list[j];
int a = node.a;
int b = node.b;
int c = node.c;
dist[b] = Math.min(dist[b], back[a] + c);
}
}
if(dist[n] > INF/2) System.out.println("impossible");
else System.out.println(dist[n]);
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String[] str1 = reader.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
k = Integer.parseInt(str1[2]);
for(int i = 0;i < m;i++)
{
String[] str2 = reader.readLine().split(" ");
int a = Integer.parseInt(str2[0]);
int b = Integer.parseInt(str2[1]);
int c = Integer.parseInt(str2[2]);
list[i] = new Node(a,b,c);
}
bellman_ford();
}
}
class Node
{
int a, b, c;
public Node(int a,int b,int c)
{
this.a = a;
this.b = b;
this.c = c;
}
}
dijkstra不能解决负权边是因为 dijkstra要求每个点被确定后st[j] = true，dist[j]就是最短距离了，之后就不能再被更新了（一锤子买卖），而如果有负权边的话，那已经确定的点的dist[j]不一定是最短了
没错
解释得通俗易懂（棒(๑•̀ㅂ•́)و✧）
爱了
赞同
好！
好！
这条评论说的有点问题。从代码看，st用在选择用哪个点来更新到其他点的距离上，而在更新距离时，还是从1到n遍历，没有任何限制。st的限制是每个点只有一次更新他能走到的点的dist的机会，并没有限制了每个点被确定距离后就不能被更新了,每个点的dist是可以多次被更新的。比如本文的第一个图，在点4后面连一个权是100的到5的边，下一步就会吧dist[4]更新成正确的1。但是这时4已经把自己唯一一次更新自己能走到的点的dist的机会用过了，所以4后面的点都不会再被更新了，只能是错误的数值了。一锤子买卖是每个点更新自己能走到的点的dist的机会只有一次，但是dist是会被多次更新。
某个点的st=true之后他自己的dist也是有可能被再次更新的，只是这个点没有了更新他后面的点的机会，已经把错误的数据传递到了后面
讲得好好哇
大佬牛逼
正确的
同学，为什么限制最多经过 k 条边就要迭代k次呢？还是说最多要迭代 k 次？
说的好啊
小呆呆%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%拿了吗
迭代一次就是找到离源点最近的点的最短路劲，k次就是离源点k条边的最短路径，这个和dijstra的两重for循环是一个意思
好哒，收到~谢谢同学
正确的，拿第二个图举例，确定了dist[4]=4，dist[5]被更新为5,后续虽然确定3号点，dist[4]更新为更小的3，但因为st[4]=true,不会再用到4去更新dist[5],答案自然是错误的.
妙啊
棒
我觉得也不一定，这个需要看代码的具体实现方式，如果说在更新每个点的距离的时候，加一个判断
if(!st[j])，这样st = true的点对应的dist就不会再更新了。其实了解原因还是得从dijkstra的证明入手，楼主的意思是当存在负权边时，每次遍历选出的最短的那个距离已经不一定是该点距离源点的最短距离了（这个是基于dijkstra算法的证明来看的，只有不存在负权边时证明才成立）。不存在负权边时，已经确定最短距离的点是否会再被其他点尝试更新已然无所谓，因为更新的距离不可能比最短距离更短（不过这个过程仍可能存在，这也是你强调的），因为带着这种想法，所以第一个例子很容易忽略最后的用点3更新第4距离的步骤，但若硬要用dijkstra来求解带负权边的图，这个过程又可能情况意外算出正确答案比如第一个例子。
是否可理解为：dijstra算法基于贪心思想，当有负权边时，局部最优不一定是全局最优
有一说一，我觉得你说的有理
赞一个
强
我感觉也是
我也觉得是
有理
## ！！！
####
这个理解强！！！牛 就是这种思想的本质
对，就一锤子买卖
有道理
good
画了一张Bellman-ford动态规划草稿图
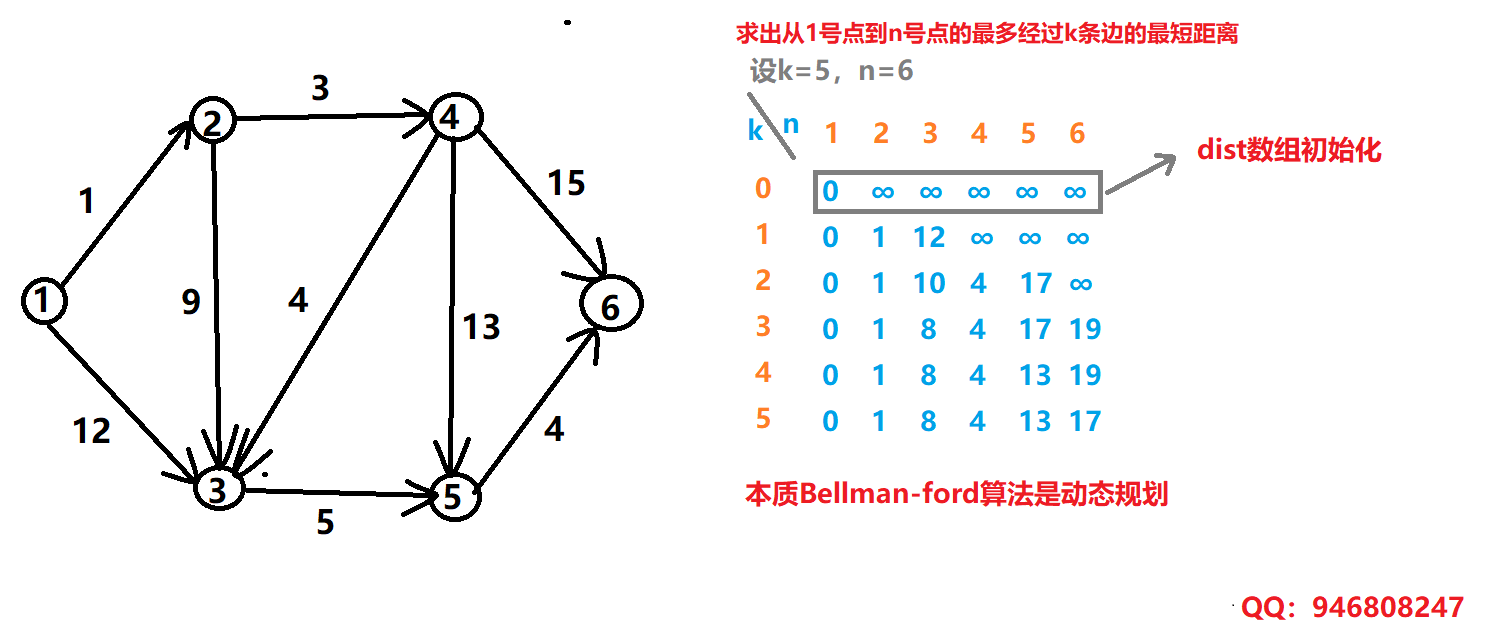
牛的
我感觉加个负权边，就更好了，你这个适合解释dijkstra，哈哈哈，
谢谢
很详细，谢谢大佬，但是你有个地方写错了，在正确的分析的dijkstra详细步骤的第2步，”2号点被更新成dist[2] = 1”，这里
dist[2]应该为2；代码如下：
输出：
已经修改，输出写得很好
dalao输出写的也太好了吧！！！
之前还不懂为什么要进行第四次循环，现在完全懂了！
那个，大佬有堆优化算法的输出吗？（狗头）
堆优化的输出和上面一样的，堆优化只是优化了如何快速找到最短距离的点，并不影响结果
呃呃，我可能是理解不了它的冗余是什么时候清，以及如何通过清理冗余得到最终的路径，这里面的细节有一些懵。
再看一次y总的视频hh
好嘞
蟹蟹大佬
太牛了大佬，小菜鸡表示原来是这么调试的
为啥啊大佬，我不确定自己理解的对不对
很棒
我想的是未优化dijkstra算法最多迭代n次， 所以每个点都会更新
我忘记当时我咋理解的了。。。。吐了
太棒了
关于外循环的作用：对所有边进行松弛操作的次数（第 i 次的意义：边数为 i 条的最短路径）那又是为什么呢？（这个想了很久，因为所有文章都是解释到上面就没接着解释了，传不了图但问题不大）
我们模拟一下可以发现，第一次循环时，对所有边松弛之后只有编号 1 的邻节点2、5的 dist 发生更新， 因为初始除了 1 其他结点的 dist 都是 +∞，1. 对于 1 的邻节点 2、5：从+∞ 更新成 w （无论 w正负一定比 +∞ 小）2. 对于除 1 的邻节点即除 2、5之外的点：对于正权边，如2-3、3-4等，一定不会更新 dist 值，因为相当于在 +∞上继续+，肯定更大；对于负权边，（假设图上有），只更新成 +∞ - w，如果最短路存在的情况下，一定不是最终的 dist
因此第一次循环只有迈一步的点（2、5）松弛成功。第二次循环，在第一次循环时松弛成功的 2、5两个点的基础上继续松弛。同理，只有迈两步的点会松弛成功。以此类推，循环k次就表示迈 k 步的点松弛成功，也就是路径更新完成，也就是从 1 号点到 n 号点的最多经过 k 条边的最短距离。
第一张和第二章图，其实推理了Dijkstra适用于有向无环图；第四点说的不太明确，课上老师讲解了具体的计算方式，500个点，10000条边，最大负权为 500W, 0x3f3f3f3约为21亿，即使除以2，也能容纳负权的可能性，因此可以除以2，这里说的随其他值变化，指向并不明确。
改成long long 为什么0x3f3f3f3f3f3f3f3f/2不行了
怎么理解松弛？
感谢大佬
为什么第一个分析错了
因为第一次用dij答案应该是1, 因为循环了n次, 最后是用3去更新了4号点的, 将原先的dis[4]变成了1, 所以这里就会提到前面y总第一次讲dij时, 有人说当t == n时是不是可以退出循环, y总说可以, 但是他没写, 这就是答案, dij用了每一个点去更新他能到达的点, 其实有一些含有负权的图(特殊情况)用dij也是可以的
有个问题，dijkstra详细步骤那第一次找到了 4 号点的距离为4，最后更新5之后不是应该return了嘛，为什么还要再去更新4号点距离为3， 不知道我想法有没有问题
应该是最多会迭代n次， 每个点都能更新
看判断，if(t==n)return ，还有个是循环完return，两种情况
感谢大佬回答~
蒟蒻
可能这就是您被y总关注的原因吧……
nb!
正确的分析下面的反例，堆优化迪杰斯特拉是能算出来的4，可以粘贴试下。
5 5
1 2 2
1 3 5
2 4 2
3 4 -2
4 5 1
Dijkstra最外层循环多循环一次 把4到5的距离在更新一下不就是1345了吗 我感觉是这样
orz
关于第一个例子我的看法, 我第一次也没看出来, 我的观点 : 第一个分析用dij答案应该是1, 因为循环了n次, 最后是用3去更新了4号点的, 将原先的dis[4]变成了1, 所以这里就会提到前面y总第一次讲dij时, 有人说当t == n时是不是可以退出循环, y总说可以, 但是他没写, 这就是答案, dij用了每一个点去更新他能到达的点, 其实有一些含有负权的图(特殊情况)用dij也是可以的
我有个小问题，使用dijstra算法前每条边加上最小负数的相反数，再使用dijstra算法不行吗
我想问一下此算法最外层的for循环就只是为了确保不出现负数边吗
第一个你觉得没有理解透彻的想法为什么我觉得是正确的，这个想法与你下面的正确分析并无大的差别
还是有问题，第一次举的例子是恰当的。