• y总题解（y总代码及其简洁！y总 yyds！！！）
  • 能用 滑动窗口 或者双指针 的话，一定具有单调性。

• Mcdull：容易理解的滑动窗口思想，力扣官方

• 相似题目：[ lc 3. 无重复字符的最长子串 & 剑指 48. 最长不含重复字符的子字符串 ]

题目

76. 最小覆盖子串

思路

• tag：滑动窗口 ，双指针

复杂度分析

• 时间复杂度：双指针只遍历一遍， 1 pass。时间复杂度 O(n)。
• 空间复杂度：哈希表中 统计字符串 s 和 t 的字符数量，题目中说 字符串 只由小写字母构成，所以最多只有 26种字符，哈希表的键 最多只有 26个。设字符集大小 为 C，这里C = 26，空间复杂度为 O(C)。
• 复杂度分析：y总文字题解

• 复杂度分析：力扣官方

代码

• 其中一个关键点：有效字符的数量cnt ++ 只会增加，不会 cnt --，因为 滑动窗口 s[ j ~ i ] 的 起点 指针 j 只有在 s[ j ] 是冗余的时候才会 向右移动，所以 指针 j 向右移动，对 有效字符 的数量 不会造成影响，有效字符数量cnt 虽然不会增加，但是也不会减少，指针 j 向右移动 只会减少 无效字符的数量。cnt ++ 靠的是 指针 i 向右移动，但是 注意 指针 i 不一定 每次向右移动 都会 使有效字符 cnt ++。
  • 第一次 找出 能覆盖 t 的 s的子串( res第一次被赋值 )时， cnt == t.size()，之后 cnt 就一直 等于 t.size() 了，不会 cnt –。也就是 res第一次被赋值 之后，每次都会进入 if (cnt == t.size()) 的判断，但是 只有 进一步 满足 i - j + 1 < res.size()， res 才能被 再次赋值。
• 自己想的一个 形象的比喻，指针 i 的作用是 开源，负责 增加有效字符cnt 的数量，助力 有效字符数量 cnt 早日达到 t.size()； 指针 j 的作用是 节流，负责 将 指针 i 开辟的疆土 中 无价值的部分 即 冗余的字符 回收，达到 最小 覆盖 子串的目的。

// 双指针 滑动窗口 要满足单调性。即 i, j 指针 均只能 朝着 一个方向移动, 不能朝一个方向移动 再 向另一个方向移动.
// 设滑动窗口 s[j ~ i], 设 指针 i 为 滑动窗口的 终点, 指针 j 为 滑动窗口的 起点.
// 设 哈希表 hw(hash_window) 存的是 滑动窗口内 各字符的数量, ht存的是 字符串t内各字符数量.
//
// 问题 1 ：如何 快速判断 滑动窗口 s[j ~ i] 内 是否 已经包含了 t内所有字符了呢(每种字符可能重复)？
// 滑动窗口 内的 有效字符 总数量 cnt = t.size(), 就说明已经包含了 t 内所有字符.
// 问题 2 ：那么 什么是 有效字符呢?
// 如果 此时 新加入了 s[i]字符之后, hw[s[i]] <= ht[s[i]], 此时的字符 s[i]有用, 就算有效字符, cnt ++.
// 如果 新加入了 s[i]字符之后, 有 hw[s[i]] > ht[s[i]] 了, 说明加入当前字符s[i] 之前, 滑动窗口内 s[i]的数量
// --- 就已经 达到了 t内这个字符s[i]的数量, 原本关于 字符s[i] 就已经达标, 现在再加就是冗余, 就是无效字符.
//
// 问题 3 ：滑动窗口 s[j ~ i]的 起点 指针 j 什么时候 才 向右 移动？
// 如果 s[j]处的字符 (字符记为#) 的数量 大于 t 中 这个字符 # 的数量, 即 hw[s[j]] > ht[s[j]],
// --- j 就可以向右移动, 因为 s[j] 处的字符 # 的数量 冗余了, j 向右移动的时候, 同时 将 hw[s[j]] --

// 问题 4 : 有效字符的数量 cnt 变化是靠的什么呢？
// cnt ++ 只能通过 指针 i 向右移动, 但是 注意 指针 i  不一定 每次 向右移动 都会 使有效字符 cnt ++。
// 指针 j 向右移动 不会影响 有效字符cnt 的数量, 即 虽然不会 cnt ++, 但是也不会出现 导致cnt --.
//
// 问题 5 : 指针 i 和 指针 j 的作用, 这里 打个 形象的比喻 ~~~
// 指针 i 的作用是 开源，负责 增加有效字符cnt 的数量, 开疆破土, 助力 有效字符数量 cnt 早日达到 t.size()； 
// 指针 j 的作用是 节流，负责 将 指针 i 开辟的疆土 中 无价值 的部分 即 冗余的字符 回收，达到 最小 覆盖子串的目的。
//
// 问题 6 ：双指针工作的流程 是 怎样的呢？ 明白了 指针 j 和 i 的作用 就很好理解啦 ~ 
// (1) 肯定是 指针 i 先移动, hw[s[i]] ++, 然后看看 是否 会 增加 cnt, 通过 if (hw[s[i]] <= ht[s[i]]) 来判断
// (2) i 每次向右移动一步之后, 每次 i 移动之后 都可能会导致 cnt == t.size(), 因为题目是求 最小 覆盖子串, 所以
// --- 在 判断 if (cnt == t.size()) 之前 要 先 用 j 将 无用的 字符回收, 达到 最小覆盖子串 的目的
// --- j 就负责 看看 i 之前开辟的疆土里面有没有 冗余的字符, 有的话就回收, hw[s[j]] -- 同时 j ++ 
// (3) i 每次开辟完新的疆土 同时 j 也回收了 可能存在的 无价值的 冗余字符, 就可以判断 cnt == t.size()啦 ~~ 

class Solution {
public:
    string minWindow(string s, string t) {
        // hw 存的是 滑动窗口内 各字符数量, ht 存的是 字符串t 的 各字符数量
        unordered_map<char, int> hw, ht; // 也可开一个哈希表作差,但是开两个思路更清晰
        for (auto c: t) ht[c] ++ ; // 统计 字符串 t 中 各字符 数量

        string res;

        int cnt = 0; // 注意: cnt 中 存的是 有效字符的数量

        for (int i = 0, j = 0; i < s.size(); i ++ ) {
            // (1) 指针 i 先移动, hw[s[i]] ++, 然后看看 是否 会 增加 cnt, 通过 if (hw[s[i]] <= ht[s[i]]) 来判断
            hw[s[i]] ++ ;
            if (hw[s[i]] <= ht[s[i]]) cnt ++ ;

            // (2) j 就负责 看看 i 之前开辟的疆土里面有没有 冗余的字符, 有的话就回收, hw[s[j]] -- 同时 j ++ 
            // 每次 i 移动完 之后, 判断 j 能不能向右移动, 注意 j 可以连续移动, 用while 不是 if
            // while (hw[s[j]] > ht[s[j]]) hw[s[j ++ ]] -- ; // 是 while, 不是 if
             while (j <= i && hw[s[j]] > ht[s[j]]) hw[s[j ++ ]] -- ; // 加上 j <= i,防止字符串下标越界

            // (3) i 每次开辟完新的疆土 同时 j 也回收了 可能存在的 无价值的 冗余字符, 就可以判断 cnt == t.size()啦
            if (cnt == t.size()) { // 更新答案
                if (res.empty() || i - j + 1 < res.size()) // 注意 res.empty()
                    res = s.substr(j, i - j + 1);
            }
        }

        return res;
    }
};

代码中 需要注意的小地方，

1. 搞清楚 什么情况下 res 才会更新？ 有两种情况：

// 这样写 出错的原因: 一开始 res.size() == 0, 不可能有 i-j+1 < 0
// 只能 第一次 res 赋值 之后, 再用 i-j+1 < res.size() 来判断
// if (cnt == t.size() && i - j + 1 < res.size())
//     res = s.substr(j, i - j + 1);

// 有效字符数cnt == t.size() 后 res 赋值的情况有两种:
// 1. res为空时, 是 第 1 次赋值
// 2. res.size() 变小后, 是 第 2, 3, 4, 5....次赋值
if (cnt == t.size())
    if (res.empty() || i - j + 1 < res.size())
        res = s.substr(j, i - j + 1);

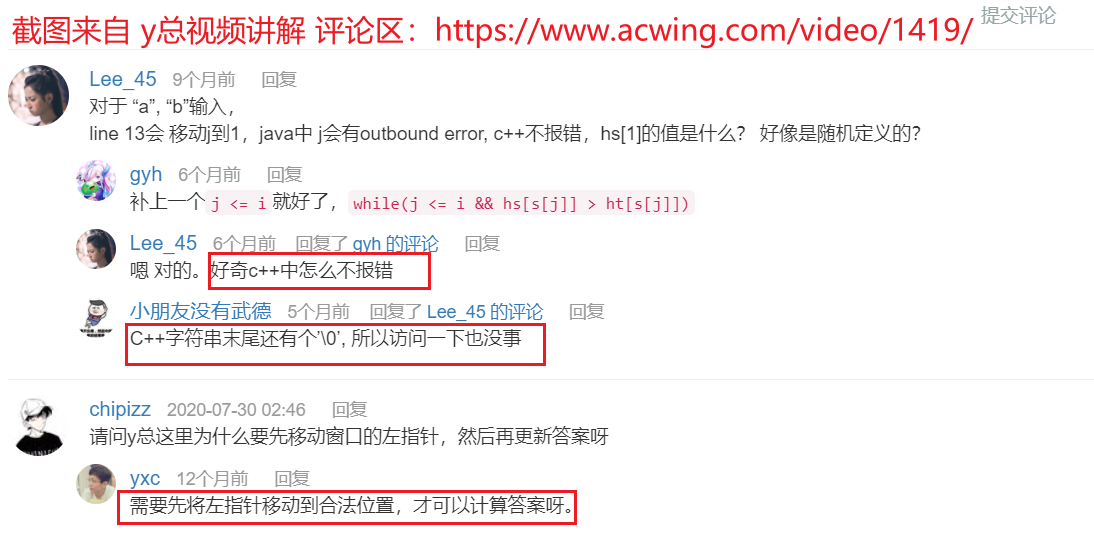
2. 防止下标越界,来自 y总视频讲解 评论区：

• while (hw[s[j]] > ht[s[j]]) hw[s[j ++ ]] -- ; 处 为了严谨，防止字符串下标越界 可以加上 j <= i，变为while ( j <= i && hw[s[j]] > ht[s[j]]) hw[s[j ++ ]] -- ;。
  • 举例：s = “a”, t = “b”