题目描述

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting directly the vertices fromi and toi.

Return the probability that after t seconds the frog is on the vertex target.

样例

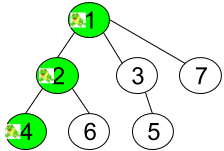
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666. 

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1. 

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

• 1 <= n <= 100
• edges.length == n-1
• edges[i].length == 2
• 1 <= edges[i][0], edges[i][1] <= n
• 1 <= t <= 50
• 1 <= target <= n
• Answers within 10^-5 of the actual value will be accepted as correct.

算法1

(BFS+路径输出) $O(N + E)$

这道题虽然给的标签是DFS，但是我采用的是BFS来求解。

这道题首先去明确题意，从节点1出发，到节点标记为target的点，从一个节点跳到另一个节点耗时1秒，问能否在规定的时间t内到达。容易引发错误的是跳跃规则的限制，首先已经经过的点是不能再跳了，另外，如果在时间t内已经到达target，但是已经没有其他的点可以继续跳跃了，那么就原地不动。后一个条件就容易引发错误，考虑这样一个例子：

n = 8, edges = [[1,2],[1,7],[1,4],[1,5],[7,8],[2,3],[4,6]], t = 20, target = 7
Output: 0.0

这是因为第一步就可以跳到target = 7，这里只用了1秒，还未到时间t，所以还可以继续跳跃到节点8，无法再跳跃了，于是落在了节点8，不符合题目要求了。

分析清楚了题意，那么问题的关键点就是最少需要跳多少步可以从节点1到节点target，所以很自然的联想到了BFS，但是还需要额外输出路径。这是因为我们最终要计算的是概率，不妨以第一个测试用例为例：

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333

从节点1到节点target = 4，节点1的跳跃选择有3个，从节点2的跳跃选择有2个，所以最终结果就是1/(2*3)=1/6。可以发现，分母恰好是每一次跳跃时，当前节点的可以选择跳跃的节点个数，所以只有确切的知道整个跳跃过程经过了哪些点，才能够统计可以跳跃的节点个数。

注意到给出的图是无向图，那么我们可以采用邻接表来表示图，用数组used来记录当前点是否被访问过，同时用来记录从出发点到终点的距离。在BFS过程中，可以从target出发找节点1，也可以从节点1出发找target，我选择是前一种。

当得到节点1和target的距离used[1]后，我们用变量pathLen来存储这个数据。如果节点1和target不相连，或者最少跳跃的时间大于t，输出0；如果used[1] <= t，就需要去处理达到target还可以继续跳跃的情况了，那么这时候就再次利用used数组，标记已经经过的点。用sum来记录最终结果的分母，注意防止溢出。

C++ 代码

class Solution {
public:
    double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);
        //特殊情况，只有1个节点
        if (edges.size() == 0) {
            return 1;
        }

        vector<vector<int>> ground(n + 1); //无向图的邻接表表示
        for (auto e : edges) {
            int from = e[0];
            int to = e[1];
            ground[from].push_back(to);
            ground[to].push_back(from);
        }

        vector<int> used(n + 1, -1); //记录节点是否被使用，同时记录跳跃的距离
        vector<int> pre(n + 1, -1); //记录当前节点是从哪个节点跳跃过来
        queue<int> q;
        q.push(target);
        used[target] = 0;

        while (!q.empty()) {
            int from = q.front(); q.pop();
            for (int i = 0; i < ground[from].size(); ++i) {
                int tmp = ground[from][i];
                if (used[tmp] == -1) {
                    q.push(tmp);
                    used[tmp] = used[from] + 1;
                    pre[tmp] = from;
                    if (tmp == 1) break;
                }
            }
        }
        //如果节点1和target不相连，或者最少跳跃的时间大于t，输出0
        if (pre[1] == -1 || used[1] > t) return 0;
        //保存从节点1到taget的时间，因为used接下来会被初始化再利用
        int pathLen = used[1];

        long long sum = 1; //防止相乘出现溢出
        int start = 1;
        fill(used.begin(), used.end(), 0);

        while (pre[start] != -1) {
            used[start] = 1;
            long long cnt = 0;
            for (int i = 0; i < ground[start].size(); ++i) {
                int to = ground[start][i];
                if (!used[to]) ++cnt;
            }
            sum *= cnt;
            start = pre[start];
        }
        //pathLen != t意味着可能存在继续跳跃的可能
        //检验是否存在从target还能继续跳到其他点
        if (pathLen != t) {
            for (int i = 0; i < ground[target].size(); ++i) {
                int to = ground[target][i];
                if (!used[to]) return 0;
            }
        }

        return 1.0 / sum;
    }
};