• y总题解（优先队列法）

• 力扣官方 （分治合并法 和 优先队列法）

• 相似题目：简化版 [lc 21. 合并两个有序链表 & 剑指 25. 合并两个排序的链表]

题目

23. 合并K个升序链表

思路

• 优先队列合并：时间 O(kn * logk), 优先队列空间 O(k)

• 分治合并法 : 时间 O(kn * logk), 递归栈空间 O(logk)

• 分治合并法的基础：合并两个有序链表 [lc 21. 合并两个有序链表 & 剑指 25. 合并两个排序的链表]

// 合并两个有序链表 迭代法：时间O(n + m), 空间O(1)
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        // dummy是指针,下面要return dummy->next. new指针要开辟内存. 内存消耗 大
        // auto dummy = new ListNode(-1), cur = dummy;

        // dummy是ListNode 型, 不是ListNode * 型, 要return dummy.next. 内存消耗 小
        ListNode dummy, *cur = &dummy; 

        while (l1 && l2) // 可以把 while的 "{}" 去掉, if-else 算是一对语句
            if (l1->val < l2->val) cur = cur->next = l1, l1 = l1->next;
            else cur = cur->next = l2, l2 = l2->next;

        cur->next = l1 ? l1 : l2;

        // return dummy->next; // dummy 是指针类型, 是 ListNode * 型
        return dummy.next; // dummy 不是指针类型, 是 ListNode 型
    }
};

代码

1. 优先队列合并：时间 O(kn * logk), 空间 O(k)

• 截图 来自 y总代码评论区 ：

• 截图 来自 y总视频讲解评论区：

• c++优先队列(priority_queue)用法详解，优先队列定义：priority_queue<Type, Container, Functional>
• for (auto l : lists) if (l) heap.push(l); 优先队列 只是把 每个链表的 头结点的地址 push进去了，而不是 把 整个链表 push进去。
  • 因为 优先队列中存的是 链表头结点的地址, 我们要比较的是结点的值 而不是 地址，所以 要自己定义 Cmp 比较 结点的值。
  • 重载 "()" 原因参考 y总代码评论区 ：STL容器 在比较的时候用的是 结构体的小括号运算符。
  • return a->val > b->val; ，注意此处 小根堆 是 ‘>’, a在b前面 表示 a在b下面。

// y总 优先队列法: 时间 O(kn * logk), 空间 O(k)
class Solution {
public:
    // 重载 "()" 是因为 STL容器 在比较的时候用的是 结构体的小括号运算符
    struct Cmp { // 重载 小括号 "()"
        bool operator() (ListNode* a, ListNode* b) {
            return a->val > b->val; // 小根堆 是 '>', a在b前面 表示 a在b下面
        }
    }; // 注意 此处 有个 ';', 很容易忘记

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        // 优先队列 定义：priority_queue<Type, Container, Functional>
        // 因为 优先队列中存的是 链表头结点的地址, 我们要比较的是结点的值 而不是 地址
        // 所以 要自己定义 Cmp 比较 结点的值
        priority_queue<ListNode*, vector<ListNode*>, Cmp> heap;

        // auto dummy = new ListNode(-1), cur = dummy; // return dummy->next
        ListNode dummy, *cur = &dummy; // return dummy.next

        for (auto l : lists) if (l) heap.push(l);

        while (!heap.empty()) {
            auto t = heap.top(); heap.pop();

            cur = cur->next = t;

            if (t->next) heap.push(t->next);
        }

        // return dummy->next; // ListNode dummy, *cur = &dummy;
        return dummy.next; // ListNode dummy, *cur = &dummy;
    }
};

2. 分治合并：时间 O(kn * logk), 递归栈空间 O(logk)

• 力扣官方

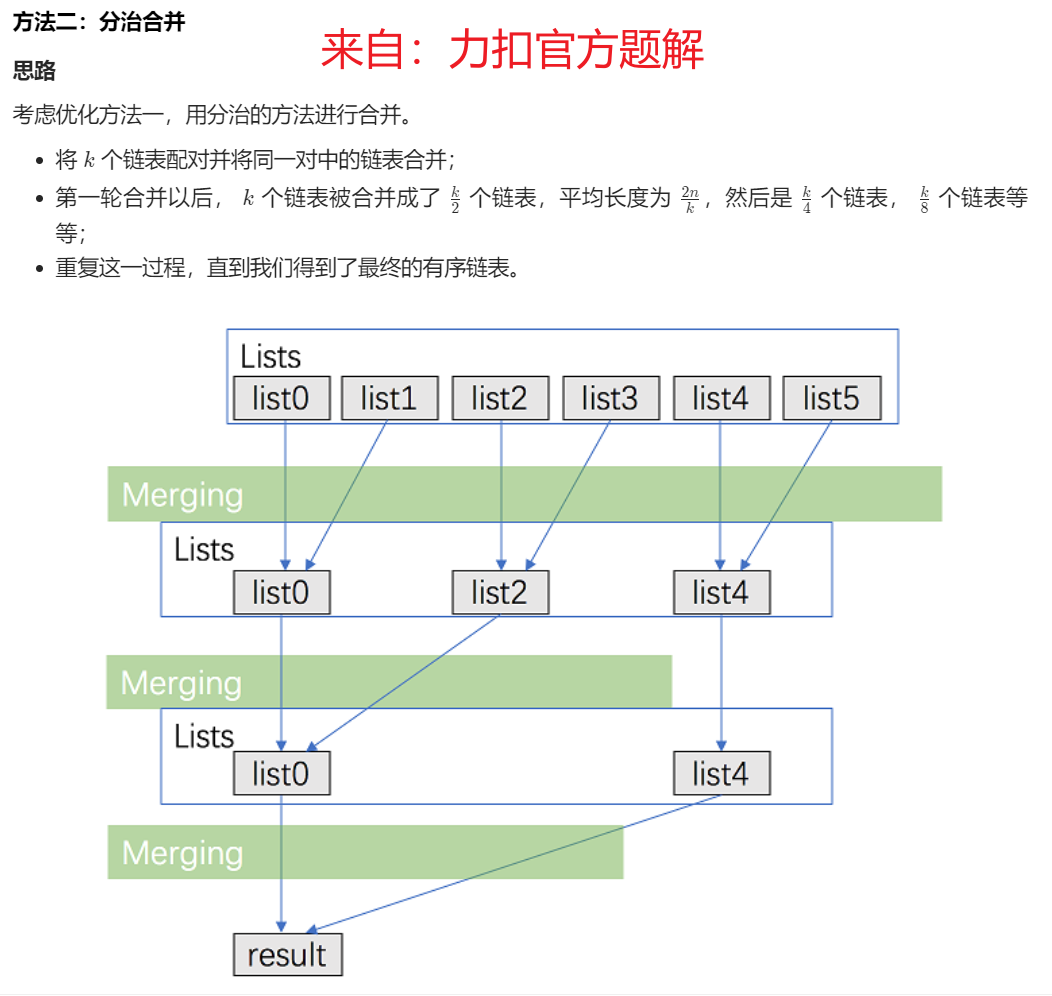
• 注意：可以不把 head 设为 ListNode * 指针类型, 而是把 head 设为 ListNode 类型，这样 就不用 考虑 内存的问题了。不把 head作为指针 new出来 确实会 节省内存，内存消耗 由 22.1MB 变为 12.7MB。 详细说明 见 题解。

// 分治合并：时间 O(kn * logk), 递归栈空间 O(logk)
class Solution {
public:
    ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
        // dummy是指针,下面要return dummy->next. new指针要开辟内存. 内存消耗 22.1MB
        // auto dummy = new ListNode(-1), cur = dummy;

        // dummy是ListNode 型, 不是ListNode * 型, 要return dummy.next. 内存消耗 12.7MB
        ListNode dummy, *cur = &dummy; 

        while (a && b) // 可以把 while的 "{}" 去掉, if-else 算是一对语句
            if (a->val < b->val) cur = cur->next = a, a = a->next;
            else cur = cur->next = b, b = b->next;

        cur->next = a ? a : b;

        // return dummy->next; // dummy 是指针类型, ListNode * 型
        return dummy.next; // dummy 不是指针类型, ListNode 型
    }

    ListNode* merge(vector <ListNode*> &lists, int l, int r) {
        if (l == r) return lists[l]; // 递归结束条件, [l, r]中 只剩下一个链表, l==r
        // if (l > r) return nullptr; // 只需要 一开始 特判 n 为 0
        int mid = (l + r) >> 1;
        return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int n = lists.size();
        if (!n) return nullptr; // 特判 n == 0
        return merge(lists, 0, n - 1); // 不用特判 n 为 1
    }
};

• 如果 想 合并 上面的 ListNode* mergeKLists() 和 ListNode* merge(). 参考 wzc1995 改成如下代码所示，不过内存消耗 增加了，变成了 28.5MB。

// 合并 上面的 ListNode* mergeKLists() 和 ListNode* merge(). 内存消耗: 28.5MB
ListNode* mergeKLists(vector<ListNode*>& lists) {
    int n = lists.size();
    if (!n) return nullptr;
    if (n == 1) return lists[0];

    int mid = n >> 1;

    auto left = vector<ListNode*>(lists.begin(), lists.begin() + mid);
    auto right = vector<ListNode*>(lists.begin() + mid, lists.end());

    auto l1 = mergeKLists(left);
    auto l2 = mergeKLists(right);

    return mergeTwoLists(l1, l2);
}