算法分析

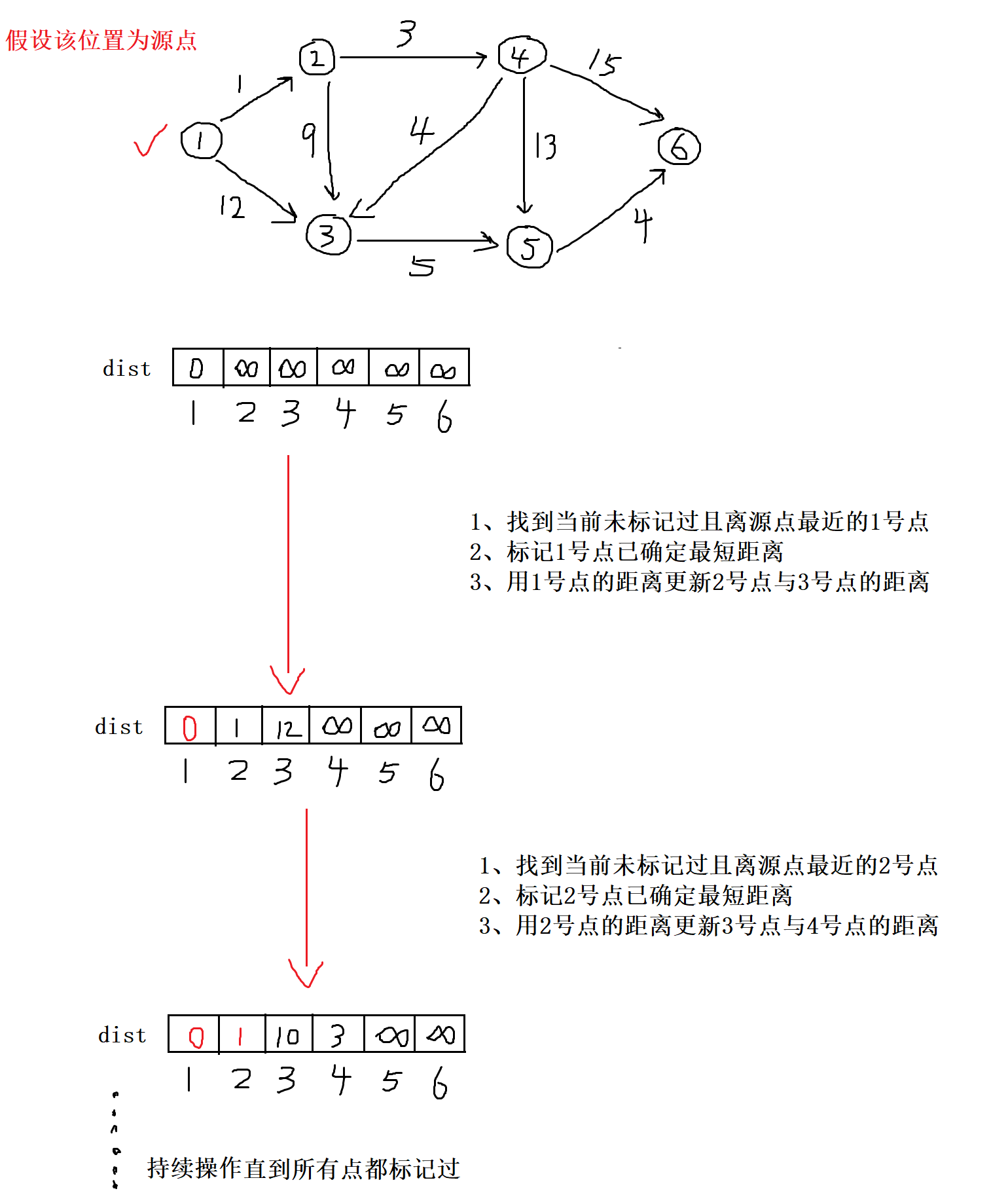
注意：若要求任意点i到任意个点j的最短距离，只需修改dijkstra方法中的起源位置dist[i] = 0，以及返回为dist[j]

时间复杂度 $O(mlogn)$

每次找到最小距离的点沿着边更新其他的点，若dist[j] > distance + w[i]，表示可以更新dist[j]，更新后再把j点和对应的距离放入小根堆中。由于点的个数是n，边的个数是m，在极限情况下（稠密图$m = \frac{n(n - 1)}{2}$）最多可以更新m回，每一回最多可以更新$n$个点（严格上是n - 1个点），有m回，因此最多可以把$n^2$个点放入到小根堆中，因此每一次更新小根堆排序的情况是$O(log(n^2))$，一共最多m次更新，因此总的时间复杂度上限是$O(mlog((n^2))) = O(2mlogn) = O(mlogn)$

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.PriorityQueue;

public class Main{
    static int N = 100010;
    static int n;

    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] w = new int[N];
    static int idx = 0;
    static int[] dist = new int[N];// 存储1号点到每个点的最短距离
    static boolean[] st = new boolean[N];
    static int INF = 0x3f3f3f3f;//设置无穷大
    public static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    // 求1号点到n号点的最短路，如果不存在则返回-1
    public static int dijkstra()
    {
        //维护当前未在st中标记过且离源点最近的点
        PriorityQueue<PIIs> queue = new PriorityQueue<PIIs>();
        Arrays.fill(dist, INF);
        dist[1] = 0;
        queue.add(new PIIs(0,1));
        while(!queue.isEmpty())
        {
            //1、找到当前未在s中出现过且离源点最近的点
            PIIs p = queue.poll();
            int t = p.getSecond();
            int distance = p.getFirst();
            if(st[t]) continue;
            //2、将该点进行标记
            st[t] = true;
            //3、用t更新其他点的距离
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                if(dist[j] > distance + w[i])
                {
                    dist[j] = distance + w[i];
                    queue.add(new PIIs(dist[j],j));
                }
            }

        }
        if(dist[n] == INF) return -1;
        return dist[n];
    }

    public static void main(String[] args) throws IOException{
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] str1 = reader.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        int m = Integer.parseInt(str1[1]);
        Arrays.fill(h, -1);
        while(m -- > 0)
        {
            String[] str2 = reader.readLine().split(" ");
            int a = Integer.parseInt(str2[0]);
            int b = Integer.parseInt(str2[1]);
            int c = Integer.parseInt(str2[2]);
            add(a,b,c);
        }
        System.out.println(dijkstra());
    }
}

class PIIs implements Comparable<PIIs>{
    private int first;//距离值
    private int second;//点编号

    public int getFirst()
    {
        return this.first;
    }
    public int getSecond()
    {
        return this.second;
    }
    public PIIs(int first,int second)
    {
        this.first = first;
        this.second = second;
    }
    @Override
    public int compareTo(PIIs o) {
        // TODO 自动生成的方法存根
        return Integer.compare(first, o.first);
    }
}