最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个 $8\times 8$ 的棋盘，棋盘的每个小方格都有一个权值 $w_{x,y}$

每次我们可以对棋盘进行一次 横 或 竖 切，将 棋盘 分成两块矩形的 子棋盘

分割完一次后，我们可以选择两个 子棋盘 中的一个再继续 递归 操作

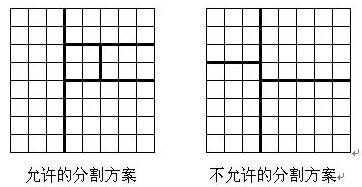
可以发现题目中给的这个图片，右边这个并不是递归下去做的：他对第一次分割的两个矩形又分别进行了分割（题目要求我们只能保留一个继续分割）

现需要把棋盘按照上述分割方案，分成 $n$ 块（$n-1$ 次划分操作）

求一个划分方案，使得各子棋盘的 总分的均方差最小

分析

本题如果用 动态规划 来分析，状态表示要至少开5维，记录分割操作的阶段，以及当前的棋盘状态

我这里直接贴出 闫氏DP分析法

闫氏DP分析法

状态表示 $f_{k,x_1,y_1,x_2,y_2}$—集合：

当前已经对棋盘进行了 $k$ 次划分，且 $k$ 次划分后选择的棋盘是 左上角为 $(x_1,y_1)$，右下角为 $(x_2,y_2)$

状态表示 $f_{k,x_1,y_1,x_2,y_2}$—属性：

划分出来的 $k + 1$ 个子矩阵的 $n\sigma^2$最小（下面给出了这样定义的原因）

状态计算 $f_{k,x_1,y_1,x_2,y_2}$：

这里关于 集合的属性 需要一点变化，直接使用 标准差 作为属性，在进行状态转移的时候不好计算

我们把标准差做出如下变化：
$$ n\sigma^2 = {\sum_{i=1}^n (x_i-\overline{X})^2} = (x_1-\overline{X})^2 + (x_2-\overline{X})^2 + \cdots + (x_n-\overline{X})^2 $$
由于 $\sigma$ 与 $n\sigma^2$ 的单调性相同，要求 $\sigma$ 最小，就相当于 $n\sigma^2$ 最小

而转化为 $n\sigma^2$ 后，对于子状态，我们就可以直接进行 加法运算 来转移了（原来套着根号很难处理）

记忆化搜索

本题有这明显的 分治 引导，即给定一个初始的棋盘，然后我们选择进行分割

分割完后，选择保留一个棋盘，然后对另一个棋盘继续进行分割

直到分割次数达到上限 $n-1$

考虑一下直接递归操作的时间复杂度：$O(\begin{pmatrix}16 \\\ n\end{pmatrix} \times n!)$

这是一个排列数，计算方法很简单，每轮会使用一条分割线，且每条分割线在一个方案里仅能使用一次

不难发现，递归操作会有很多冗余的重复计算，于是我们可以采用 记忆化搜索 进行优化

$f_{k,x_1,y_1,x_2,y_2}$ 表示对棋盘进行了 $k$ 次划分，且 $k$ 次划分后选择的棋盘是 左上角为 $(x_1,y_1)$，右下角为 $(x_2,y_2)$

这一步分析就有点雷同于上面的 DP 了

关于如何枚举矩阵的分割（会的可以直接跳过）

由于我们这里记录矩阵的状态是通过他的 对角顶点 记录的，因此分割是我们也可以通过枚举对角顶点完成分割

如下图所示：

竖着切：

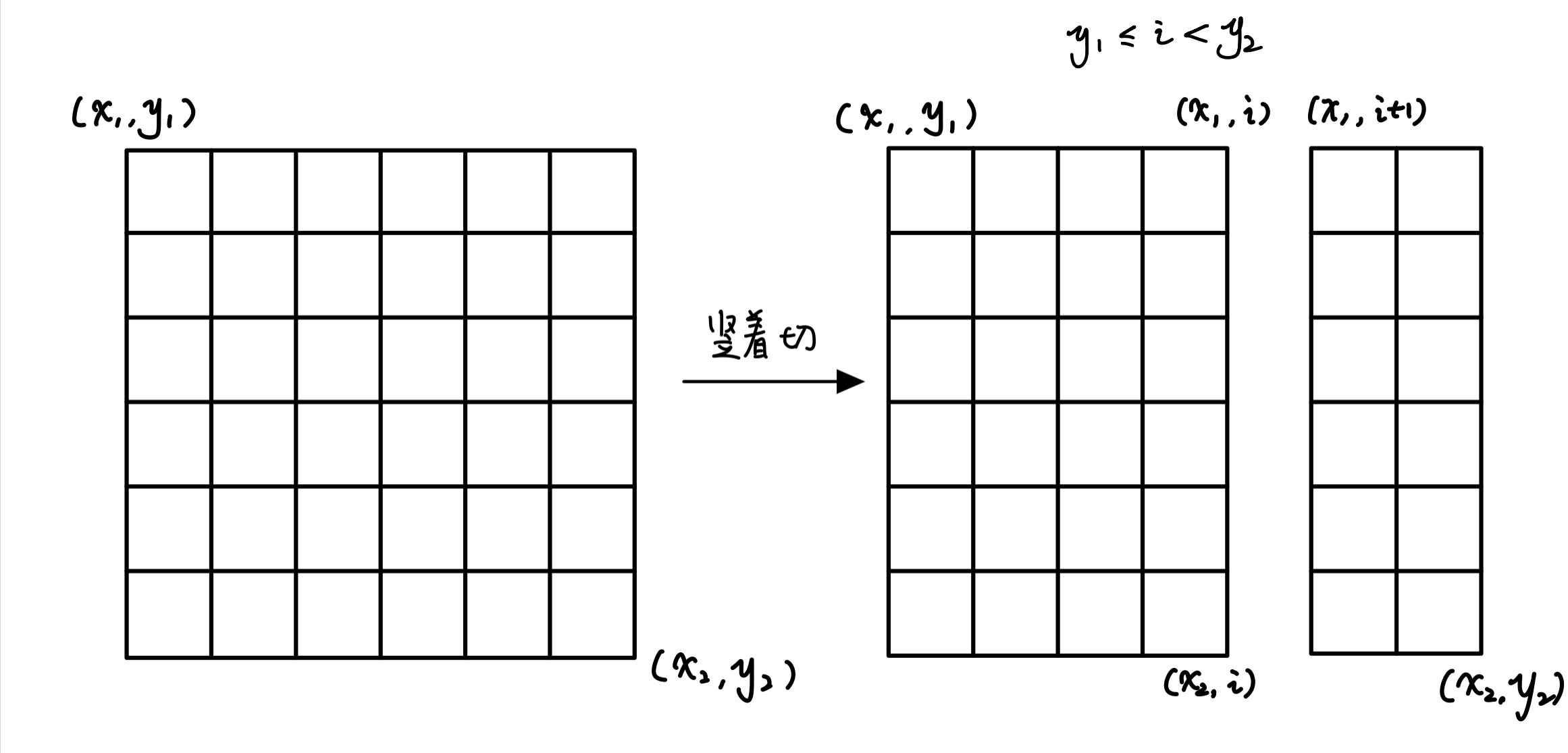
横着切：

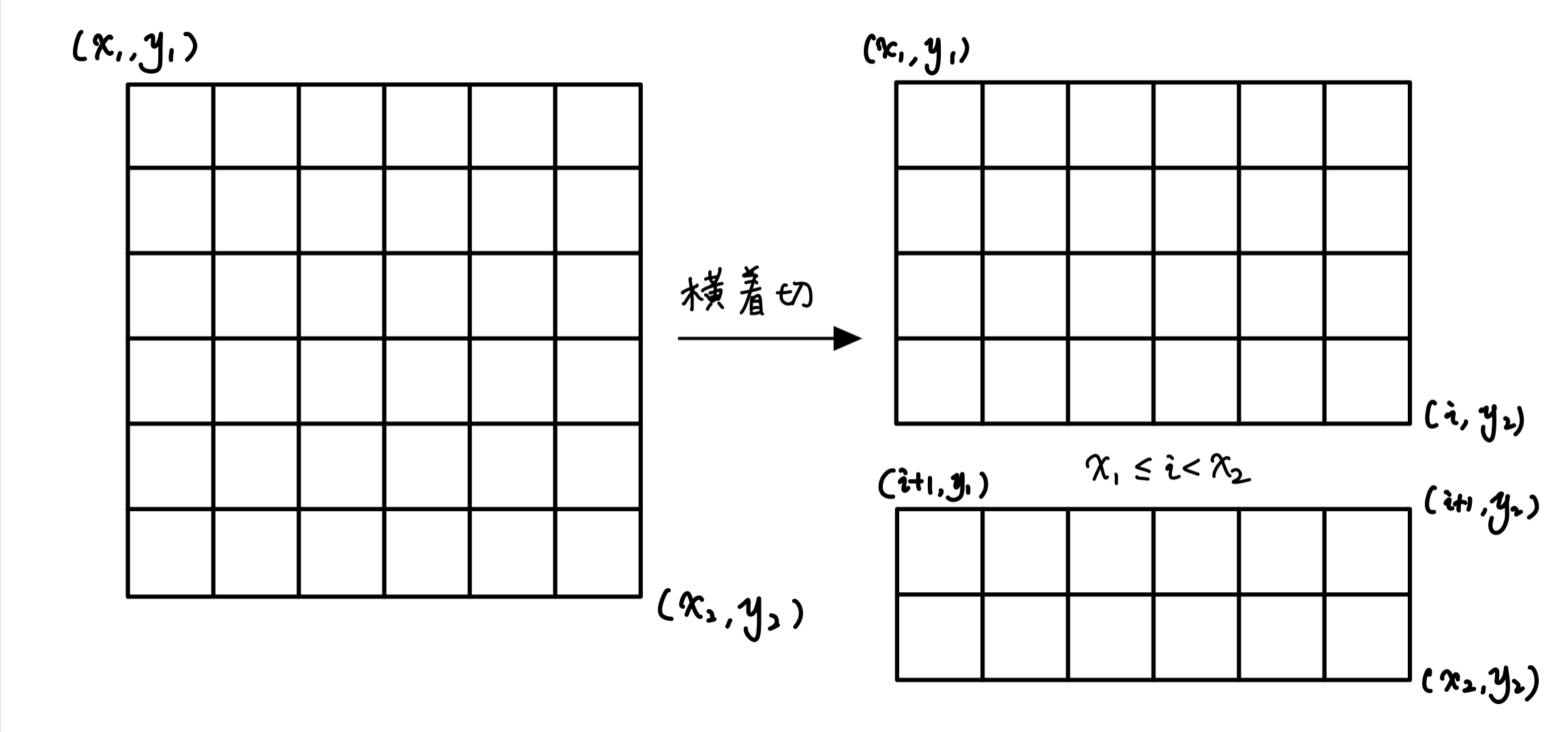
Code （记忆化搜索）

由于会频繁地计算某个矩阵的方差，因此我们需要先预处理出前缀和，保证计算方差的时间复杂度为 $O(1)$

时间复杂度 ：$O(n^5)$

我这里 阶段定义 的含义和 y总 是反过来的，读者注意区分两者的不同

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 16;
int n, m = 8;
int s[N][N];
double f[N][N][N][N][N];
double X;

double get(int x1, int y1, int x2, int y2)  //求该矩阵的 n\sigma^2
{
    double delta = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
    delta = delta - X;
    return delta * delta;
}
double dp(int k, int x1, int y1, int x2, int y2)
{
    if (f[k][x1][y1][x2][y2] >= 0) return f[k][x1][y1][x2][y2]; //记忆化搜索
    if (k == n) return f[k][x1][y1][x2][y2] = get(x1, y1, x2, y2);  //更新初始状态

    double t = 1e9; //初始化为无穷大
    for (int i = x1; i < x2; i ++ ) //横着切
    {
        t = min(t, dp(k + 1, x1, y1, i, y2) + get(i + 1, y1, x2, y2));
        t = min(t, dp(k + 1, i + 1, y1, x2, y2) + get(x1, y1, i, y2));
    }
    for (int i = y1; i < y2; i ++ ) //竖着切
    {
        t = min(t, dp(k + 1, x1, y1, x2, i) + get(x1, i + 1, x2, y2));
        t = min(t, dp(k + 1, x1, i + 1, x2, y2) + get(x1, y1, x2, i));
    }
    return f[k][x1][y1][x2][y2] = t;
}
int main()
{
    //读入
    scanf("%d", &n);
    for (int i = 1; i <= m; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);
    //预处理前缀和
    for (int i = 1; i <= m; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
    //初始化所有状态
    memset(f, -1, sizeof f);
    //计算均值X拔
    X = (double) s[m][m] / n;
    //记忆化搜索
    printf("%.3lf\n", sqrt(dp(1, 1, 1, m, m) / n));
    return 0;
}