一.欧拉函数 O(√a∗n)
对于一个大于1的自然数n来说,由算术基本定理可以将n分解为k个质数的乘积:n=pα11×pα22×…×pαkk
记欧拉函数为ϕ(n),
欧拉函数ϕ(n)解决的问题:求解1~n中与n互质的数的个数
互斥:对于两个数a与b,若a和b的公约数只有1时,称a和b互斥
欧拉函数的具体公式:ϕ(n)=n×p1−1p1×p2−1p2×…×pk−1pk
二.欧拉函数的证明:
证:
利用容斥原理来证明,如不懂,可以先看一下 小学数学:容斥原理
设sum为1~n中与n互斥
基本思路是去掉1~n中所有p1,p2,…,pk的倍数
①当p1,p2,…,pk的倍数集合没有交集时
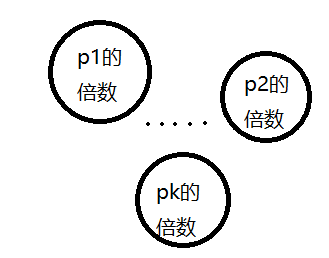
sum=n−np1−np2−…−npk
②当p1,p2,…,pk中的任意两个数的倍数集合拥有交集时
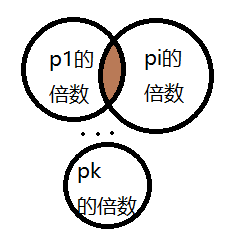
这时在第①步时,会多减一次pi×pj,所以需要加上一次pi×pj
因此有sum=n−np1−np2−…−npk+np1×p2+np1×p3+…+npk−1×pk
依次类推有③,④,…
最后将n提出来,就可出现ϕ(n)=n×p1−1p1×p2−1p2×…×pk−1pk的形式
证毕
三.时间复杂度分析:
算法的瓶颈主要在分解质因数上,分解质因数的时间复杂度为O(√a),但由于有n组数据,所以时间复杂度为O(√a∗n)
四.代码
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
while(n--)
{
int a,res;
cin>>a;
res = a;
for(int i=2;i<=a/i;i++)
{
if(a%i==0)
{
while(a%i==0)
a/=i;
res = res / i*(i-1);
}
}
if(a>1) res = res /a*(a-1);
cout<<res<<endl;
}
return 0;
}
喜欢题解的话,欢迎点赞、收藏、关注(三连)喔,如有什么疑问,欢迎评论下方指出


if(a>1) res = res /a*(a-1); 请问最后a为什么还会大于1(a最后不都是1?)
质因子大于根号n的最多有一个,因此有一个可能没分解到。a最后不一定都位1,比如10分解为2*5,最后的a就是5,5比根号10大
真是让人醍醐灌顶,好文