最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定 $n$ 个点的 凸多边形 中每个 顶点 的 权值 $w_i$

我们可以把该 凸多边形 划分成 n - 2 个 三角形（三角形不能相交，这样就能保证是 $n-2$ 了）

每次划分三角形的 费用 为 三个顶点权值 的 乘积

求一个划分 方案，$s.t.$ 方案的 费用总和 最小

分析

这是一个经典的 图形学 问题 — 三角剖分

因为我们现实中常见的一些 多边形图形 存储到计算机中，需要转存为一个个 像素点

那么如何存储一个 多边形 最简单的方案就是把它转化为 多个三角形 进行存储

也就是 三角剖分 问题，不只是 凸多边形，还能解决 凹多边形， 有孔多边形 等问题

对应有 $O(n^3)$ 的暴力算法，$O(n^2)$ 的 $ear clipping$ 算法，$O(n\log n)$ 的 $Delaunay$ 算法

还有很复杂的线性算法

以上和本题都没啥关系，大家有兴趣学习的可以自行翻阅文献和资料

回归本题，本题是一个给定的 凸多边形 求 三角剖分 的最小费用方案

很显然一个 凸多边形的剖分方案 并不唯一：

在 选定 多边形中 两个点 后，找出 三角形 的 第三个点 的方案有 $n-2$ 个

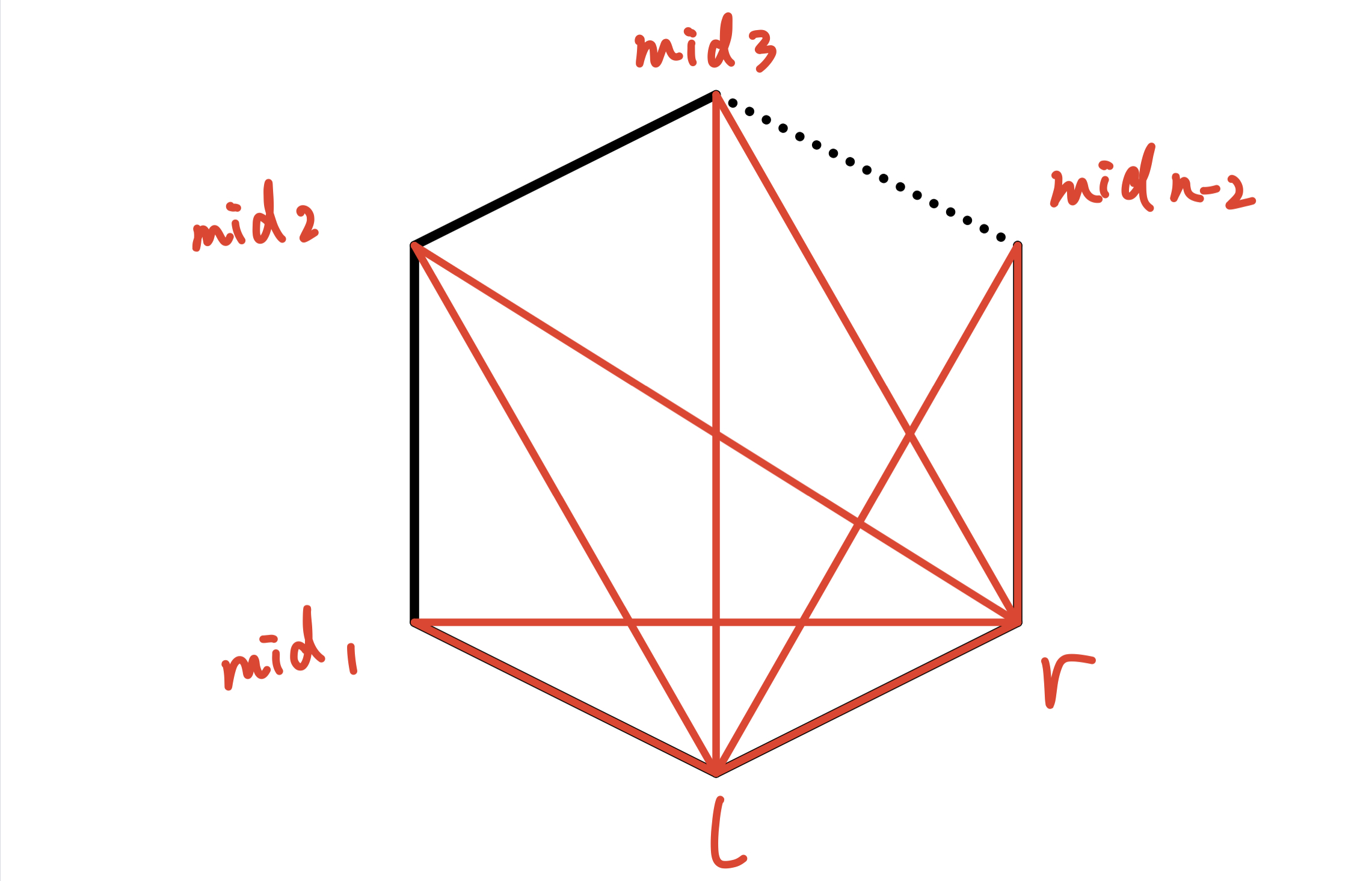
然后还要分别 划分 他的 左右两块区域

因此我们就会想到用 记忆化搜索 或者 区间DP 来进行处理

记忆化搜索介绍 可以参考这篇 加分二叉树【记忆化搜索思想】

区间DP介绍 可以参考这篇 环形石子合并【区间DP+环形区间问题】

本题解采用 区间DP 的方式进行求解

闫氏DP分析法

状态表示—集合$f_{l,r}:$ 当前划分到的多边形的左端点是 $l$，右端点是 $r$ 的方案
状态表示—属性$f_{l,r}:$ 方案的费用最小
状态计算—$f_{l,r}:$

$$ f_{l,r} = min(f_{l,k} + f_{k,r} + w_l \times w_k \times w_r) \quad (l \lt k \lt r) $$

区间DP 在状态计算的时候一定要 认真 划分好 边界 和 转移，对于不同题目是不一样的

然后本题非常的嚣张，直接用样例的 $5$ 的点告诉我们答案会爆 $int$ 和 $long long$

并且没有 取模 要求，那就只能上 高精度 了 用Python了

Code

时间复杂度： $O(n^3)$ 区间DP

#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 55;

int n;
int w[N];
vector<int> f[N][N];

bool cmp(vector<int> &a, vector<int> &b)
{
    if (a.size() != b.size()) return a.size() < b.size();
    for (int i = a.size() - 1; i >= 0; i -- )
        if (a[i] != b[i])
            return a[i] < b[i];
    return true;
}
vector<int> add(vector<int> a, vector<int> b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size() || i < b.size(); i ++ )
    {
        if (i < a.size()) t += a[i];
        if (i < b.size()) t += b[i];
        c.push_back(t % 10);
        t /= 10;
    }
    while (t) c.push_back(t % 10), t /= 10;
    return c;
}
vector<int> mul(vector<int> a, LL b)
{
    vector<int> c;
    LL t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += b * a[i];
        c.push_back(t % 10);
        t /= 10;
    }
    while (t) c.push_back(t % 10), t /= 10;
    return c;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    //区间DP
    //此处初始状态f[l][l+1] = 0 初始就是空vector，不用额外设置
    for (int len = 3; len <= n; len ++ )
    {
        for (int l = 1, r; (r = l + len - 1) <= n; l ++ )
        {
            //初始化初始状态
            for (int k = l + 1; k < r; ++ k)
            {
                //w_l * w_k * w_r
                auto new_val = mul(mul({w[l]}, w[k]), w[r]);
                //f[l][k] + f[k][r] + cost
                new_val = add(add(new_val, f[l][k]), f[k][r]);
                //f[l][r] = min(f[l][r], f[l][k] + f[k][r] + w_sum)
                if (f[l][r].empty() || cmp(new_val, f[l][r])) f[l][r] = new_val;
            }
        }
    }
    //输出最终答案
    auto res = f[1][n];
    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}