题目描述

有一个 N * N 的网格，我们在上面放一些 1 * 1 * 1 的小正方体，输入一个N * N的网格矩阵，v=grid[i][j]表示在grid(i, j)这个位置上放置v个立方体，现在我们看这些立方体在xy, yz, xz三个维度的投影，返回三个维度的投影的面积的和。

样例

输入：[[1,2],[3,4]]
输出：17
说明：见下图

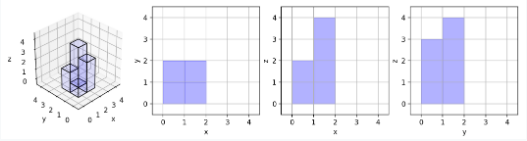
三个方向上投影的面积分别为xy=4, xz=6, yz=7，加起来和为17.

算法1

(直接计算) $O(n^2)$

分别计算每个维度上的投影面积，看示例图可知，xy维度上就是grid矩阵中非0元素的个数，xz维度上就是grid矩阵每列的最大值的和，yz维度上就是grid矩阵每行的最大值的和，遍历矩阵求得三个维度的投影的面积再相加即可。

时间复杂度分析：遍历矩阵 $O(n^2)$

C++ 代码

class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
        if(grid.size()==0)
            return 0;
        int xy = 0;
        int xz = 0;
        int yz = 0;
        int N = grid.size();
        for(int i = 0;i<N;i++){
            int max_row = 0;
            int max_col = 0;
            for(int j = 0;j<N;j++){
                if(grid[i][j]>max_row)
                    max_row = grid[i][j];
                if(grid[j][i]>max_col)
                    max_col = grid[j][i];
                if(grid[i][j]>0)
                    xy += 1;
            }
            yz += max_row;
            xz += max_col;
        }
        return xy+xz+yz;
    }
};