线段树

//传入节点编号，用子节点信息来算父节点信息
push up（int u）

//将一段区间初始化为一颗线段树
build()

//修改操作,修改某一个点或者某一个区间（懒标记）
modify()

//查询某一段区间的信息
query()

定义：

线段树是一颗满二叉树；以一棵长度为10的序列为例:

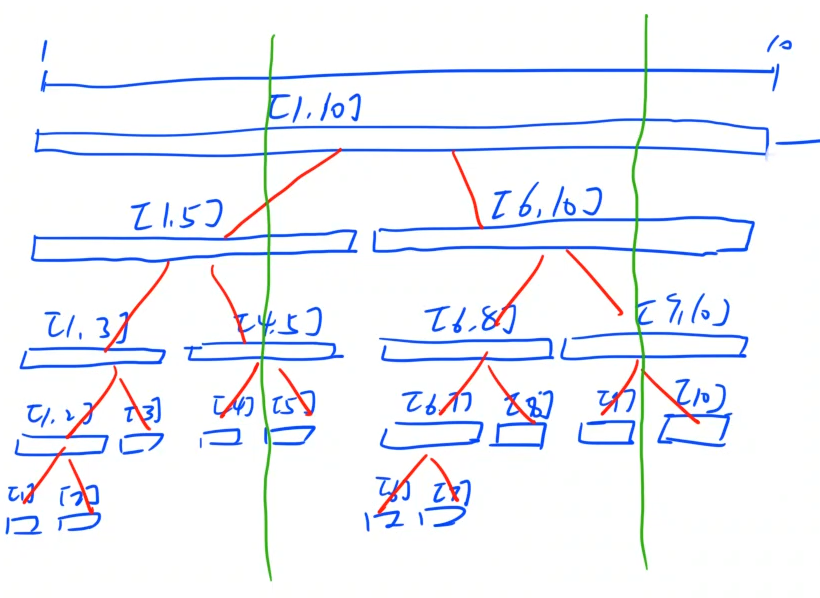
对于图中的段从上到下，从左到右依次编号为1，2，3 .....

因此某一段 u 的左儿子是 u<<1 ，右儿子是 u<<1|1 。

线段树的结构

//一般使用结构体来存储线段树,空间大小开四倍
struct Node{
    int l,r;  //维护的区间
    int v;   //维护的信息...
} tree[N*4];

线段树的建树：

//build
void build(int u,int l,int r){ //构建节点u，其维护的是区间[l,r]
    tr[u]={l,r};
    if(l==r) return ; //已经是叶子节点
    int mid=l+r>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}

push_up操作

//push_up操作,用子节点信息来更新父节点信息,以维护最大值为例
void push_up(int u){
    tree[u].v=max(tree[u<<1].v,tree[u<<1|1].v);
}

查询操作

//query操作，用来查询某一段区间内的信息,以最大值为例
int query(int u,int l,int r){  //从u节点开始查询[l,r]区间内的某一信息
    if(tree[u].l>=l&&tree[u].r<=r) return tree[u].v;  //说明这一段的信息已经被完全包含，因此不需要继续向下递归，直接返回即可
    int res=0;
    //否则需要判断该递归那一边
    int mid=tree[u].l+tree[u].r >> 1;
    if(l<=mid) res=max(res,query(u<<1,l,r));  //递归左边并更新信息
    if(mid<r) res=max(res,query(u<<1|1,l,r));  //递归右边并更新信息,切记是mid<r，无等号
    return res;
}

修改操作

//modify操作，用来修改某一叶子节点并更新其所有父节点
void modify(int u,int x,int v){   //从u节点开始递归查找，将编号为x的节点的值修改为v
    if(tree[u].l==x&&tree[u].r==x) tree[u].v=v;
    else{
        int mid=tree[u].l+tree[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        push_up(u);
    }
}

本题代码：

#include<bits/stdc++.h>
using namespace std;
#define N 200010

int m,p;

struct Node{
    int l,r;
    int v;
}tr[N*4];
//用子节点信息来更新父节点
void push_up(int u){
    tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}
//建树
void build(int u,int l,int r){
    tr[u]={l,r};
    if(l==r) return ;
    int mid=(l+r)>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
//查询操作
int query(int u,int l,int r){
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;

    int mid=tr[u].l+tr[u].r>>1;
    int v=0;
    if(mid>=l) v=max(v,query(u<<1,l,r));
    if(mid<r) v=max(v,query(u<<1|1,l,r));

    return v;
}
//修改操作
void modify(int u,int x,int v){  //将点x修改成v
    if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
    else{
        int mid=tr[u].l+tr[u].r >> 1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        push_up(u);
    }
}

int main(){
    scanf("%d%d",&m,&p);
    //建树
    build(1,1,m);

    int n=0,last=0;
    for(int i=1;i<=m;i++){
        char op[2];
        int l;
        scanf("%s%d",op,&l);
        if(op[0]=='Q'){
            last=query(1,n-l+1,n);
            printf("%d\n",last);
        }
        else{
            int v=(l+last)%p;
            modify(1,++n,v);
        }
    }
    return 0;
}