历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1057. 股票买卖 IV 原题链接中等

作者：

Shadow , 2019-11-12 09:31:00 , 所有人可见 , 阅读 2112

11

6

闫氏dp分析法之

————状态机分析法

//来自算法提高课

我自己总结的状态机分析法的过程

整个分析过程相当于图论建模
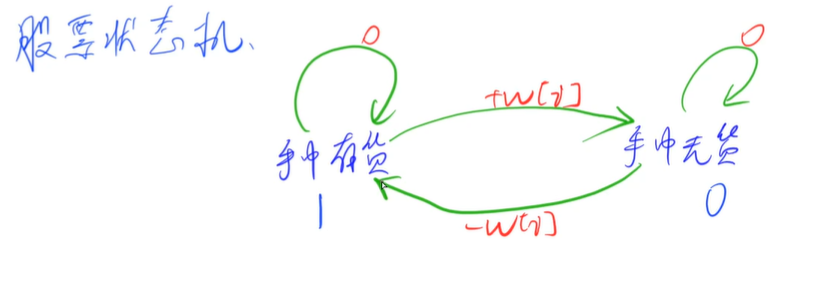
1. 首先设计状态，把几个状态画出来，作为节点
2. 然后我们考虑这几个节点之间有什么逻辑关系
并依据此给它们之间加上有向边（还有自环）
3. 之后给边加上权值
4. 最后根据每个状态的入度写出状态转移方程

用状态机怎么划分状态：

手中有票 or 手中没有票
f[i][j][0/1]
表示第i天，
已经完成了j笔交易，
现在手中有/没有票

用状态机怎么转移状态：

捕获.PNG

初始化：

如果一种状态不合法，或者不希望从这个状态转移过来，那么就把它设成正无穷或负无穷
因为这个题要求最大值，所以把不合法的设成负无穷，也这样这个状态不可能用来更新后来的状态
例如这道题中f[i][0][1]表示，如果我们处理了0笔股票，并且我们手中居然还有票，这显然是不可能的
如果我们处理了0笔股票并且目前手里没有票，那收入就是0，即f[i][0][0] = 0

所以我们将f先全置成负无穷，再单独处理为0的情况
//不合法的情况除了上面那种应该还有，但是我没想出来，dalao们求指教qwq

CODE

#include<bits/stdc++.h>
#define read(x) scanf("%d",&x)
using namespace std;
const int INF = 0x3f3f3f3f;
int n,k,a[100005],f[100005][103][2],ans;

int main(){
    read(n),read(k);
    for(register int i=1; i<=n; i++) read(a[i]);

    memset(f,-0x3f,sizeof(f)); 
    for(register int i=0; i<=n; i++) f[i][0][0] = 0;

    for(register int i=1; i<=n; i++) 
        for(register int j=1; j<=k; j++) {
            f[i][j][0] = max(f[i-1][j][0],f[i-1][j][1]+a[i]);
            f[i][j][1] = max(f[i-1][j][1],f[i-1][j-1][0]-a[i]);
        }
    for(register int i=0; i<=k; i++) ans = max(ans,f[n][i][0]);
    printf("%d\n",ans);
    return 0;
}

10 评论

ΘLLΘ 2021-04-16 22:32

大佬为啥要全部初始化为0，只法f[0][0][0]不行吗

捡到一束光 2021-02-26 11:16

补充：还有一种不合法的情况是 f[0][j][1]

希冀 2022-05-07 21:48

还有i/2<=k,也不合法

I-AK-IOI 2020-08-08 21:53

为什么不能是

f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j - 1][1] + a[i]);
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - a[i]);

Sean今天AC了吗 2020-08-19 14:11

定义一次买卖为完整的交易，所以当买入的时候为第$i$次交易，随后卖出也算作是第$i$次交易，而下一次的买入算作$i+1$次交易,下一次的卖出算作$i + 1$次交易，如果你把卖出算作是新的第$i$次交易，那么对于你的上一次买入便是 $i - 1$次交易，因为对于第一次交易而言有买入才有卖出，当$i = 1$的时候买入算作是第$0$次买卖，显然是不对的。

I-AK-IOI 2020-08-03 17:37

为什么不能是

 f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + a[i]);  
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - a[i]);

Akac 2020-08-05 11:25

好像你写的这个跟上面是一样的😂

哈哈哈hh 2020-06-17 00:36

老哥，哪错了啊，全部一样，自己写的啊

#include <iostream>
#include <cstring>
using namespace std;

const int N = 100005;
const int k = 105;

int f[N][k][2];

int a[N];
int main()
{
    memset(f,-0xcf,sizeof f);

    int n = 0;
    scanf("%d",&n);
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    for( int i=0; i<=n; i++) f[i][0][0] = 0;


    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= k; j++)
        {
            f[i][j][0] = max(f[i-1][j][0],f[i-1][j][1] + a[i]);
            f[i][j][1] = max(f[i-1][j][1],f[i-1][j-1][0] - a[i]);
        }
    }
    int res = 0;
    for(int i = 0; i <= k; i++)
    {
        res = max(res,f[n][i][0]);
    }
    cout << res << endl;
}