起点到终点恰好经过k条边的最短距离模板题-----类floyd的dp + 增量算法（类似快速幂）

本题思想与floyd的思想不一样，只是写法较接近

dp过程

$ dp[a + b,i,j]$表示从点$i$到点$j$经过$a + b$条边的最短路径

那么转移方程就是：

i ~ j所采用的边数可以转化为i ~ k用的边数 + k ~ j用的边数，两者等价

即 $ dp[a + b,i,j] = min{ d[a,i,k] + d[b,k,j] } $

计算过程与floyd基本一直，先枚举$k$，再枚举$i$和$j$

增量算法

如果我们从直接去做，我们先要枚举边数$N$，然后枚举分界点$k$,最后枚举两个端点$i,j$,那么时间复杂度即为$O(N * n^{3})$,那么必定会超时

并且我们发现每段距离都是独立的，所以具有结合律的特性，所以我们采用快速幂的思想，

倍增过程

g[ ][ ]数组初始表示只经过一条边的最短距离，然后进行倍增过程

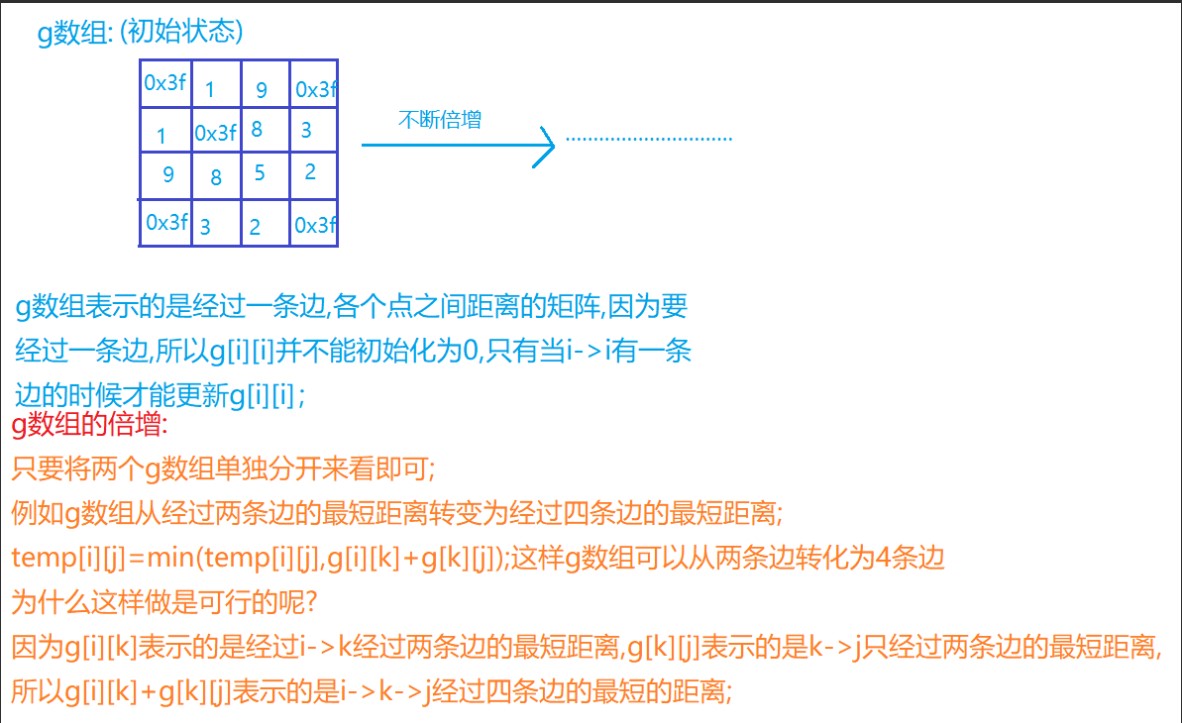
dp + 快速幂

c++代码

注意g数组初始化的时候要根据实际出发

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
const int N = 210;
int g[N][N];   //初始时表示只有一条边的最短距离
int res[N][N]; 
map<int,int> ids;
int k,m,S,E; //k表示需要k条边，m表示边的个数,S,E表示起点和终点
int n; //表示离散化之后节点的编号

void mul(int a[][N],int b[][N],int c[][N]){ //倍增函数吗,使用的边长条数即为

    static int temp[N][N];
    memset(temp,0x3f,sizeof temp);

    for(int k = 1;k <= n;++k){
        for(int i = 1;i <= n;++i){
            for(int j = 1;j <= n;++j){
                if(temp[i][j] > b[i][k] + c[k][j]){
                    temp[i][j] = b[i][k] + c[k][j];
                }
            }
        }
    }

    //注意不能用参数的来做初始化长度，因为是一个指针
    memcpy(a,temp,sizeof temp);

}


void qmi(){  //快速幂求使用k条边时对应的dist数组

    memset(res,0x3f,sizeof res);
    for(int i=1;i<=n;i++) res[i][i]=0;

    while(k){
        if(k & 1) mul(res,g,res);  //res = g * res，相当于g数组对应使用的边数 + res数组对应使用的边数

        mul(g,g,g); //将g数组更新到下一个二进制数

        k >>= 1;
    }
}

int main(){
    cin >> k >> m >> S >> E;

    //先要进行离散化
    if(ids.count(S) == 0) ids[S] = ++n;
    if(ids.count(E) == 0) ids[E] = ++n;

    memset(g,0x3f,sizeof g);
    //因为g数组必须走过一条边,所以g[i][i]不初始化为0,除非i->i之间有边

    S = ids[S] , E = ids[E];

    for(int i = 0;i < m;++i){
        int a,b,c;
        cin >> c >> a >> b;
        //离散化
        if(ids.count(a) == 0) ids[a] = ++n;
        if(ids.count(b) == 0) ids[b] = ++n;
        a = ids[a] , b = ids[b];
        g[a][b] = g[b][a] = min(g[a][b],c);
    }

    qmi();  //用快速幂求k经过k条边

    cout << res[S][E] << endl;
    return 0;
}