这就是那道，y总说要加进提高课里，但是一直没有加的题目

题目描述

初始时，一共有 $n$ 个颜色为 $0$ 馒头，然后我们一共要操作 $m$ 次

每次使得第 $(i×p+q)modN+1 $ 个和第 $(i×q+p)modN+1$ 个之间的馒头染上颜色 $i$

最终输出每个馒头的颜色

分析

本题直接翻译成大白话的意思就是，给定一个区间，每次使该区间的某个子区间的所有元素值变成 $i$

问经过 $m$ 次操作后，该区间内每个元素的值为多少

一开始读完题，都会想到用一些 数据结构，例如 Splay 或者 Segment tree 来做模拟

我也都试了试，最后发现本题的 数据规模 令人绝望，$1 \le M \le 10^7$

而 splay 和 segment tree 的 区间修改 时间复杂度为 $O(\log n)$

因此毫无疑问会被卡掉（结尾我会把我T了的代码也贴上来，供大家参考）

针对于该 数据规模，我们需要想到一些线性的做法

已知 正着推，模拟的最优时间复杂度为 $O(m\log n)$，所有我们不妨想一想 倒着推 会不会好一点

观察到一个明显的性质：

1. 如果正着枚举，那么任意阶段中每个馒头的颜色都不是唯一确定的（可能下个阶段就被染成新的了）
2. 如果倒着枚举，那么如果当前馒头已被染上颜色，则他的颜色就是被唯一确定下来的了（最后一次被染色的操作）

那么本题就转化成了 区间覆盖模型 了，即每次把覆盖的区间删掉，最终把整个区间覆盖的模型

在本题里就是，每次把染色的区间删掉 并 记录该颜色，最后输出每个元素的颜色（没删的为 $0$）

这是一个 并查集 的 经典应用

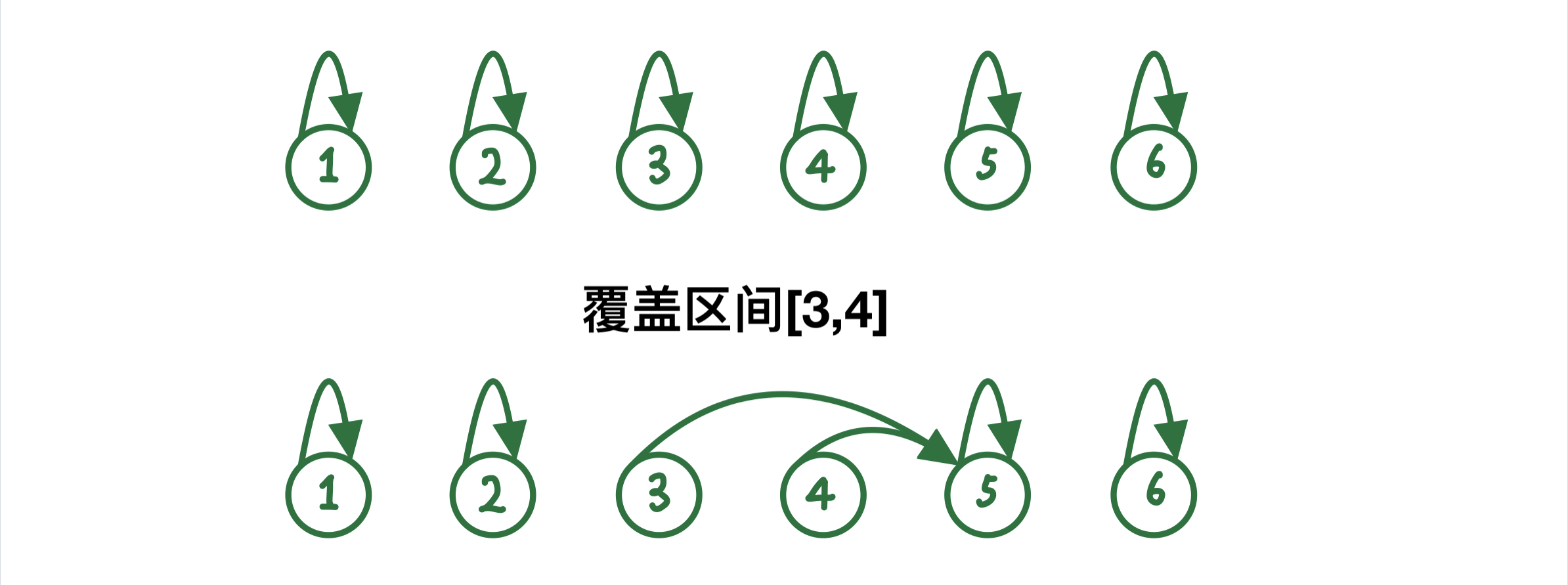
用 $p_i$ 记录第 $i$ 个元素后面第一个 未被覆盖 的区间的 左端点

覆盖一个元素的方法就是，把 $p_{p_i}$ 更新成右边的 $p_{i+1}$ 即可

覆盖一个区间 $[l,r]$ 的方法类似，把该段里所有的 $p_{p_i}$ 都更新成$p_{r+1}$

这样直接搞，看上去是 $O(mn)$ 的，但是我们在覆盖区间的时候，是可以进行 指针跳跃 的

即删完一段后就跳到整段后面，再删后面一段 p[pa] = find(pa + 1);pa = find(pa); 具体参考下面代码

这样每进行一次 覆盖，保证了 连通块 就会 减少一个，因此最多不会超过 $n$ 次 覆盖操作

覆盖操作的具体图示如下：

这里贴出一些相似的题目供大家熟悉该模型：

1. AcWing 1242. 修改数组
2. AcWing 3820. 未出现过的最小正整数

当然倒着做的时候也可以用 Segment Tree 维护

但是需要在一个区间被完全覆盖之后，不在遍历该节点，达成 剪枝 的操作

那么 最坏时间复杂度 就是把线段树所有结点都更新的时间复杂度：$O(n\log n)$，而不是正推的 $O(m\log n)$

Code（并查集—区间覆盖模型）

时间复杂度： （理论）$O(m \log n)$

但是 y 总告诉我们，笔试的时候要说并查集时间复杂度为$O(\log n)$，上机的时候看做 $O(1)$ 就好啦~

时间复杂度： （玄学）$O(m)$

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m, _p, q;
int p[N], color[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &_p, &q);
    for (int i = 1; i <= n + 1; ++ i) p[i] = i;
    for (int i = m; i; -- i)
    {
        int a = (i * q + _p) % n + 1;
        int b = (i * _p + q) % n + 1;
        int l = min(a, b), r = max(a, b);
        int pa = find(l);
        while (pa <= r)
        {
            color[pa] = i;
            p[pa] = find(pa + 1);
            pa = find(pa);
        }
    }
    for (int i = 1; i <= n; ++ i) printf("%d\n", color[i]);
    return 0;
}

Code（线段树—倒着推剪枝）

时间复杂度： $O(n \log n)$

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m, p, q;
struct Node
{
    int l, r, v;
}tr[N << 2];
int color[N];

void pushup(int u)
{
    if (tr[u << 1].v && tr[u << 1 | 1].v)
    {
        tr[u].v = true;
    }
}
void build(int u, int l, int r)
{
    tr[u] = {l, r, 0};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void modify(int u, int l, int r, int v)
{
    if (tr[u].v) return;//这个区间已经被染色了,就剪枝剪掉
    if (tr[u].l == tr[u].r) tr[u].v = v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, v);
        if (r > mid) modify(u << 1 | 1, l, r, v);
        pushup(u);
    }
}
void output(int u)
{
    if (tr[u].l == tr[u].r) printf("%d\n", tr[u].v);
    else output(u << 1), output(u << 1 | 1);
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &p, &q);
    build(1, 1, n);
    for (int i = m; i; -- i)
    {
        int l = (i * p + q) % n + 1, r = (i * q + p) % n + 1;
        if (l > r) swap(l, r);
        modify(1, l, r, i);
    }
    output(1);
    return 0;
}

Code（Splay正着推）

过了 $60\%$

#include <iostream>

#define lson tr[u].s[0]
#define rson tr[u].s[1]

using namespace std;

const int N = 1e6 + 10;

int n, m, p, q;
struct Node
{
    int s[2], v, p, c, size, flag;
    void init(int _v, int _p) {v = _v, p = _p;}
}tr[N];
int root, idx;

void pushup(int u)
{
    tr[u].size = tr[lson].size + tr[rson].size + 1;
}
void pushdown(int u)
{
    if (tr[u].flag)
    {
        tr[u].c = tr[u].flag;
        tr[lson].flag = tr[u].flag;
        tr[rson].flag = tr[u].flag;
        tr[u].flag = 0;
    }
}
void rotate(int x)
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}
void splay(int x, int k)
{
    while (tr[x].p != k)
    {
        int y = tr[x].p, z = tr[y].p;
        if (z != k)
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
    if (!k) root = x;
}
void insert(int v)
{
    int u = root, p = 0;
    while (u) p = u, u = tr[u].s[v > tr[u].v];
    u = ++ idx;
    if (p) tr[p].s[v > tr[p].v] = u;
    tr[u].init(v, p);
    splay(u, 0);
}
int get_k(int k)
{
    int u = root;
    while (true)
    {
        pushdown(u);
        if (tr[lson].size >= k) u = lson;
        else if (tr[lson].size + 1 == k) return u;
        else k -= tr[lson].size + 1, u = rson;
    }
    return -1;
}
void output(int u)
{
    pushdown(u);
    if (tr[u].s[0]) output(tr[u].s[0]);
    if (1 <= tr[u].v && tr[u].v <= n) printf("%d\n", tr[u].c);
    if (tr[u].s[1]) output(tr[u].s[1]);
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &p, &q);
    for (int i = 0; i <= n + 1; ++ i) insert(i);
    for (int i = 1; i <= m; ++ i)
    {
        int l = (i * p + q) % n + 1, r = (i * q + p) % n + 1;
        if (l > r) swap(l, r);
        l = get_k(l), r = get_k(r + 2);
        splay(l, 0), splay(r, l);
        tr[tr[r].s[0]].flag = i;
    }
    output(root);
    return 0;
}

Code（线段树正着推）

过了 $80\%$

是不是说明 $Splay$ 常数比 $Segment Tree$ 大？

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m, p, q;
struct Node
{
    int l, r, v, flag;
}tr[N << 2];

void pushup(int u)
{
    if (tr[u << 1].v == tr[u << 1 | 1].v) tr[u].v = tr[u << 1].v;
    else tr[u].v = -1;
}
void pushdown(int u)
{
    if (tr[u].flag)
    {
        tr[u << 1].v = tr[u].flag;
        tr[u << 1].flag = tr[u].flag;
        tr[u << 1 | 1].v = tr[u].flag;
        tr[u << 1 | 1].flag = tr[u].flag;
        tr[u].flag = 0;
    }
}
void build(int u, int l, int r)
{
    tr[u] = {l, r, 0};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}
void modify(int u, int l, int r, int v)
{
    if (l <= tr[u].l && tr[u].r <= r)
    {
        tr[u].v = v;
        tr[u].flag = v;
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, v);
        if (r > mid) modify(u << 1 | 1, l, r, v);
        pushup(u);
    }
}
int query(int u, int k)
{
    if (tr[u].l <= k && k <= tr[u].r && ~tr[u].v) return tr[u].v;
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (k <= mid) return query(u << 1, k);
    return query(u << 1 | 1, k);
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &p, &q);
    build(1, 1, n);
    for (int i = 1; i <= m; ++ i)
    {
        int l = (i * p + q) % n + 1, r = (i * q + p) % n + 1;
        if (l > r) swap(l, r);
        modify(1, l, r, i);
    }
    for (int i = 1; i <= n; ++ i) printf("%d\n", query(1, i));
    return 0;
}