最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

区间DP 重复度太高了，想写一点不一样的东西hh

给定一个含有 $n$ 个结点的二叉树的 中序遍历 序列中每个节点的 权值

定义一棵 子树 的 分数 为 $左子树的分数 \times 右子树的分数 + 根节点的权值$

额外规定 空树 的 分数 为 $1$

求一种满足该 中序遍历 的建树方案，使得整棵树的 分数 最大

分析

因为本题是一道与树相关的区间DP，因此本题解采用 记忆化搜索 的思想来分析，抛开常规 动态规划 思路

首先读者需要知道一个二叉树的小常识：

二叉树节点 向下投影，映射成的数组序列就是 中序遍历序列，入下图所示

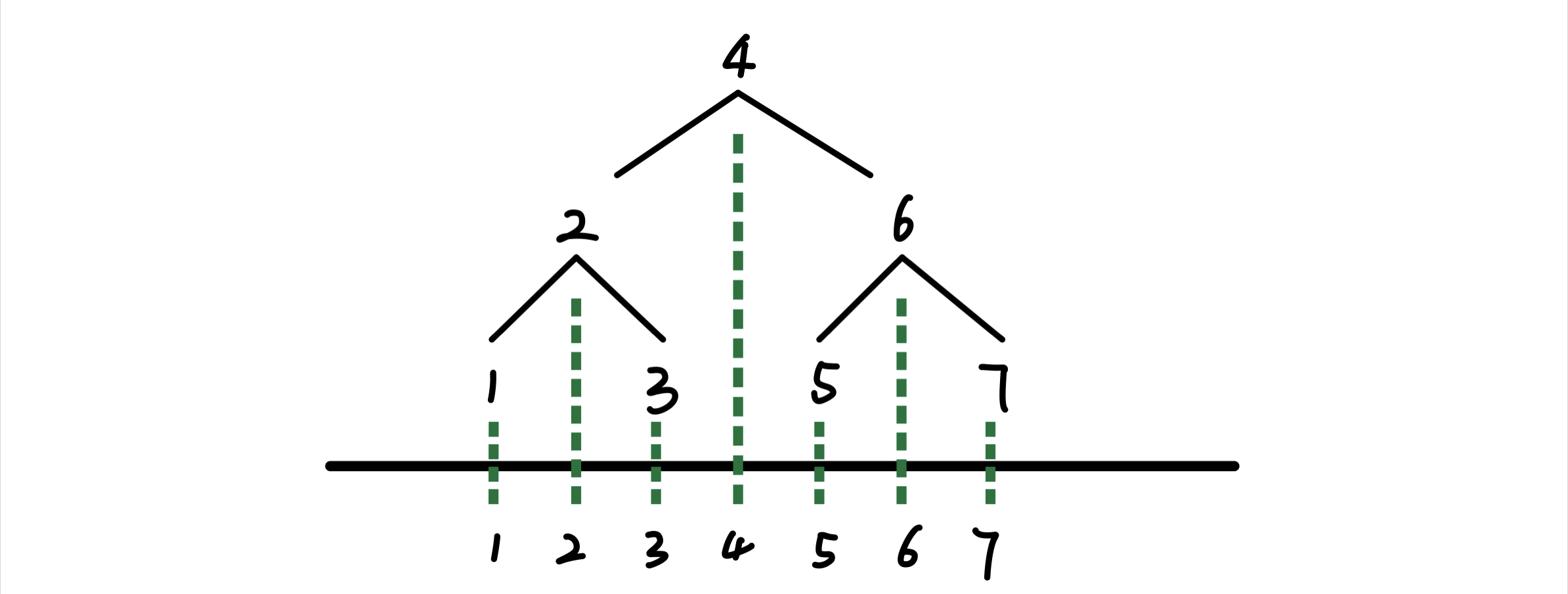
这也是诱使我们本题采用 区间DP 的一大原因之一（但这篇题解采用 记忆化搜索 思想分析）

借助上图直观的表象，我们发现可以任意的选择 中序遍历 的某一段区间便可生成多棵子树（枚举根节点）

于是我们就会想到 分治 的思想，枚举好根节点后，递归的处理左右区间生成的 最大分数子树

回溯后，利用计算好的子树的分数 相乘，再加上根结点的 权值，就可以得出该方案的 最大分数

而直接递归 搜索 的时间复杂度是 $O(n!)$（每次枚举当前区间的根结点，然后递归处理左右区间）

$n \times (n-1) \times \cdots \times 1 = n!$ （每次向下层递归时，会确定一个根节点，因此每次少 $1$）

因为在这个递归中，有相当大的计算是去处理的 相同的区间

因此我们不妨采用 记忆化搜索 的形式优化掉这些 重复的搜索

考虑用数组 $f_{l,r}$ 记录以 $l$ 为左端点，$r$ 为右端点的区间，生成的树的最大分数

这样就会 剪枝 掉相当大的冗余 搜索分支

关于输出方案这里就不做过多阐述了，想了解的可以看一下下面两篇博客

1. 递归写法：AcWing 1013. 机器分配【分组背包+背包DP输出方案—拓扑图分析】
2. 迭代写法：AcWing 12. 背包问题求具体方案【01背包 + 背包DP输出方案

Code（记忆化搜索）

时间复杂度：$O(n^3)$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 35, INF = 0x3f3f3f3f;

int n;
int w[N];
int f[N][N], g[N][N];

int dp(int l, int r)
{
    if (~f[l][r]) return f[l][r];                    //记忆化搜索
    if (l == r) return g[l][r] = l, f[l][r] = w[l];  //题设只有一个节点时，分数就是权值
    if (l > r) return f[l][r] = 1;                   //题设空子树的分数为1
    int score = -INF;
    for (int root = l, t; root <= r; ++ root)
        if ((t = dp(l, root - 1) * dp(root + 1, r) + w[root]) > score)
            score = t, g[l][r] = root;
    return f[l][r] = score;
}
void dfs(int l, int r)
{
    if (l > r) return;
    cout << g[l][r] << " ";
    dfs(l, g[l][r] - 1);
    dfs(g[l][r] + 1, r);
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];
    memset(f, -1, sizeof f);
    cout << dp(1, n) << endl;
    dfs(1, n);
    return 0;
}

秉持着详细全面的态度，我这里也贴出 闫氏DP分析法 ，但是关于 DP 就不做分析啦，都是裸的 区间DP

闫氏DP分析法

状态表示—集合$f_{l,r}:$ 当前以 $l$ 为左端点，$r$ 为右端点的区间作为 中序遍历，生成树的方案
状态表示—属性$f_{l,r}:$ 方案的分数最大
状态计算—$f_{l,r}:$

$$ f_{l,r} = max(f_{l,k - 1} \times f_{k + 1, r} + w_k) \quad (l \le k \lt r) $$

初始状态： $f_{l,l} = w_l$ 题设规定只有一个节点的子树分数就是其权值
目标状态： $f_{l,r}$

Code（区间DP）

时间复杂度：$O(n^3)$

#include <iostream>
using namespace std;

const int N = 31;
int n;
int w[N];
int f[N][N];
int g[N][N];
//g(l, r)用于记录(l, r)区间内的根结点

void dfs(int left, int right) {
    if (left > right) return;
    int root = g[left][right];
    //前序遍历，根-左-右
    cout << root << " ";
    dfs(left, root - 1);
    dfs(root + 1, right);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];

    for (int i = 1; i <= n; ++i) f[i][i] = w[i], g[i][i] = i;
    //叶结点的权值是本身，这是题目规定的
    //初始化f和g
    //当然这个可以写进循环里，特判len==1的情况，我这样写是便于理解
    //具体代码可以看我在寒假每日一题中加分二叉树题目的打卡

    for (int len = 2; len <= n; ++len) {
        for (int l = 1; l + len - 1 <= n; ++l) {
            int r = l + len - 1;
            for (int k = l; k <= r; ++k) {
                int l_tr = k == l ? 1 : f[l][k - 1];
                int r_tr = k == r ? 1 : f[k + 1][r];
                int score = l_tr * r_tr + w[k];
                if (score > f[l][r]) {
                    f[l][r] = score;
                    g[l][r] = k;
                }
            }
        }
    }
    cout << f[1][n] << endl;
    dfs(1, n);

    return 0;
}