最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

之前写的太水了，删掉了，这题的状态表示要换个角度来理解

给定 $N$ 个能量石，每个能量石有一个二元属性 $(w_{i,1}, w_{i,2})$

其中 $w_{i,1}$ 表示第 $i$ 个能量石和第 $i-1$ 个能量石融合产生的 能量 的其中一个参数

当然 $w_{i,2}$ 表示第 $i$ 个能量石和第 $i+1$ 个能量石融合产生的 能量 的其中一个参数

魔法石是顺序且环形摆放的，每次可以融合相邻两个魔法石

融合两个能量石 $i,i+1$ 所产生的能量为（题目保证，相邻能量石的参数一致，首尾一致）

$$ E_{i,i+1} = w_{i,1} \times (w_{i,2} 或 w_{i+1,1}) \times w_{i+1,1} $$

融合后左侧魔法石的第一个参数和右侧魔法石的第二个参数合并成为一颗新的 魔法石

具体如下图所示：

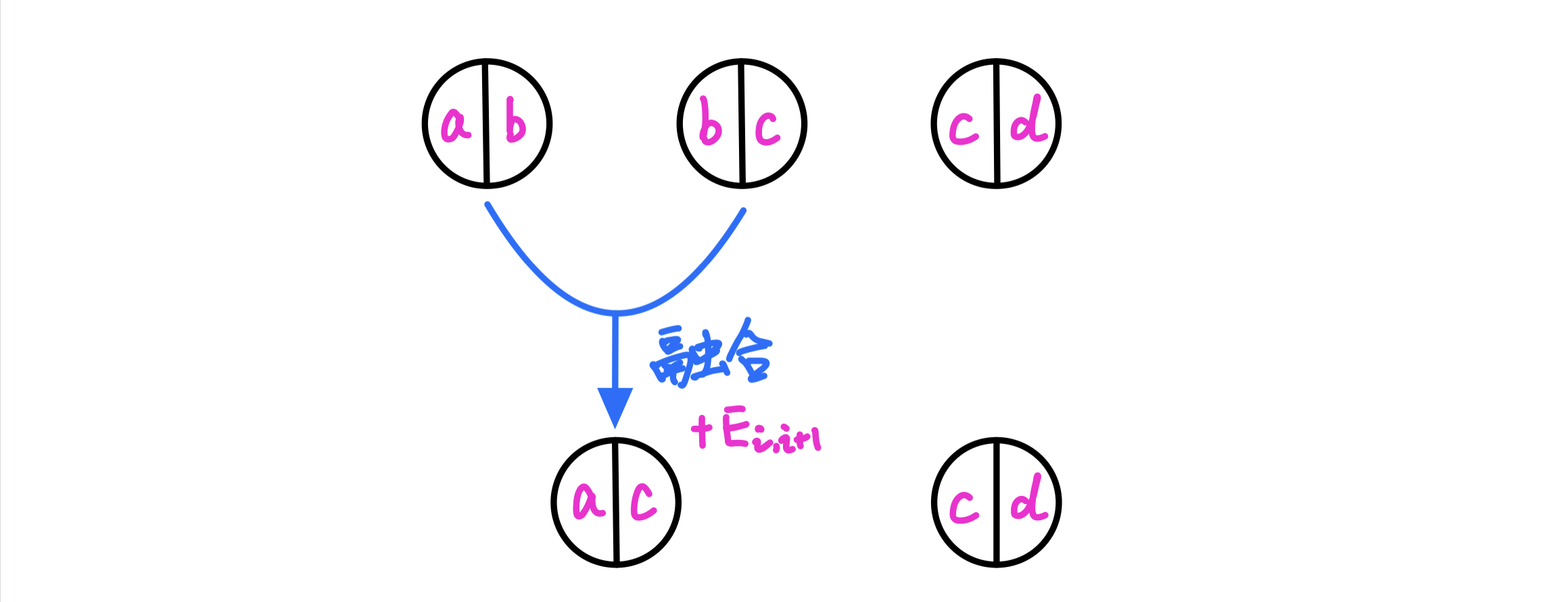
求最终把所有石头融合成一个石头时，产生的最大能量值

分析

本题可以把区间长度作为搜索的阶段来进行记忆话搜索，因此我们也可以采用 区间DP 的方式来处理

这题和 环形石子合并 十分相似，但又不尽相同

在 环形石子 中，每个石头只有单一的参数，而本题有两个参数，也就意味着我们需要在细节上做出改变

经过观察我们发现，合并两个石头 $(a,b),(b,c)$ 的操作就像是矩阵乘法一样，合并完后就变成了 $(a,c)$

因此我们可以离散的来存储每个参数，具体如下所示：

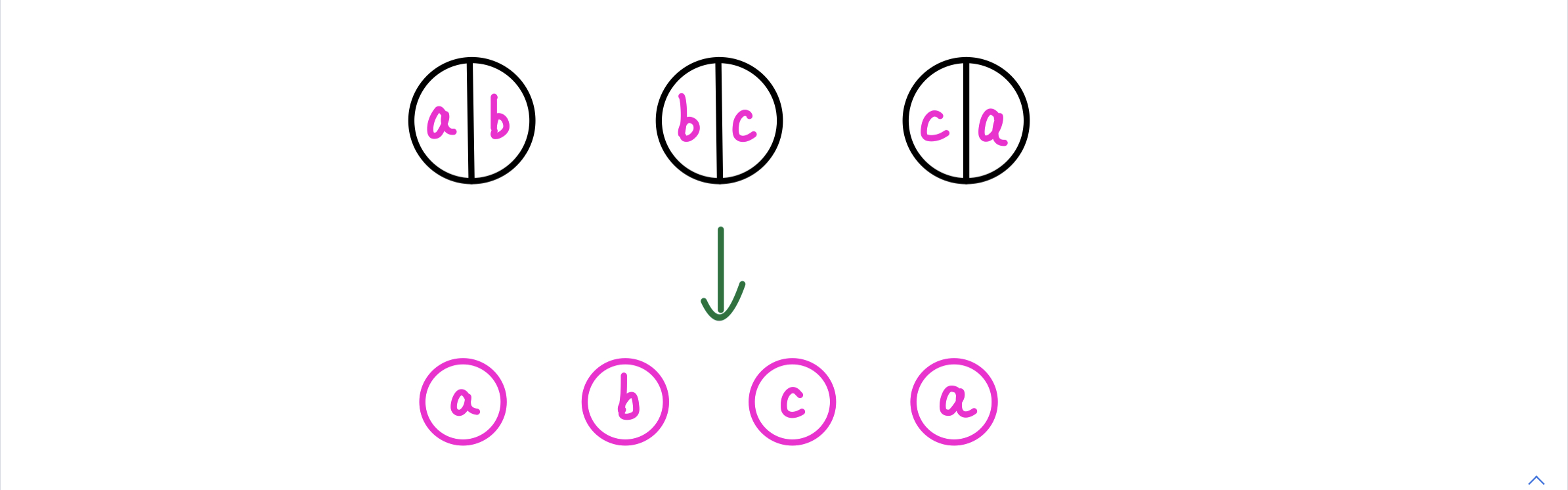
这样 状态表示 就更新为：当前合并的石子堆的左端石头的左参数是 $l$，右端石头的右参数是 $r$ 的方案

这样对应的 初始状态 本来应该是一个有着 二元属性 的石头，现在就变成了长度为 $2$ 的区间

这样合并区间后，需要记录的新石头的参数也刚好是 区间的两端 对应的参数，如下图所示：

而且这里我们的转移方程也要修改为 $f_{l,r} = max(f_{l,k} + f_{k,r} + E_{l,r})$

以往的 区间DP 我们是把区间 $[a,b]$ 拆分为 $[a,k] 和 [k+1,b]$

因为 同一个石子 只会被合并到 一个石子堆 里

但本题合并魔法石时，分割点 $k$ 要被分到 左侧石子堆的右端点 和 右侧石子堆的左端点 中

因此，参数 $k$ 要作为两个区间的共同端点来使用，即 $[a,k]$ 和 $[k,b]$

此外我们原来只需要合并 $n$ 个石头，这样转换后就要合并 $n+1$ 个石头了

具体分析如下所示：

闫氏DP分析法

状态表示—集合$f_{l,r}:$ 当前合并的石子堆的左端石头的左参数是 $l$，右端石头的右参数是 $r$ 的方案
状态表示—属性$f_{l,r}:$ 方案的费用最大
状态计算—$f_{l,r}:$

$$ f_{l,r} = max(f_{l,k} + f_{k,r} + E_{l,r}) \quad (l \lt k \lt r) $$

初始状态： $f_{l,l+1} = 0 \quad(1\le l \le n)$

目标状态： $f_{1,n + 1}$

本题关于如何解决 环的问题 不做额外阐述，有需要的可以参考之前写的这篇 环形石子合并

Code

时间复杂度： $O(n^3)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110, M = N << 1;

int n, w[M], f[M][M];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i) scanf("%d", &w[i]), w[n + i] = w[i];
    memset(f, -0x3f, sizeof f); //本题可以不用初始化，因为不存在负数的状态值，因此0就是最小的
    for (int len = 2; len <= n + 1; ++ len)
        for (int l = 1, r; (r = l + len - 1) <= n << 1; ++ l)
            if (len == 2) f[l][r] = 0; //初始化初始状态
            else
                for (int k = l + 1; k < r; ++ k)
                    f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
    int res = 0;
    for (int l = 1; l <= n; ++ l) res = max(res, f[l][l + n]);
    printf("%d\n", res);
    return 0;
}