最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个 $n$ 个点，$m$ 条边且连通的 无向图

初始时，无向图中没有边，每个 点 都是 互不连通 的

我们初始可以选择任意一个点作为 起点，且该选择 起点 的操作 费用 是 $0$

然后开始维护这个包含起点的 连通块

每次我们选择一个与 连通块内的点 相连的一条边，使得该边的另一个点（本不在连通块内的点）加入连通块

该次选边操作的费用是：$边权 \times 该点到起点的简单路径中经过的点数$

最终我们的目标是，使得 所有点都加入当前的连通块内

求解一个 方案 ，在达成目标的情况下，费用最小，输出方案的费用

分析

这题我试着预处理了一下合法状态和合法转移，结果爆MLE了
说明本题的时间复杂度也处在一个极限的情况下，暂时没有更好的优化思路了

题目要求已经连通的两点之间无须连接额外的边（这个条件其实不用给，可以推出来）
即我们只需选择 $n-1$ 条边即可

因此，我们的目标是：找出图中的 最小生成树

但本题的 最小生成树 和广义的最小生成树不同

因为在本题中，加入连通块的费用是随当前点到起点的路径线性变化的 (设经过的点数为 $k$，则费用为$w \times k$)

计算该次加边的费用是用到了如下两个参数：

1. 起点
2. 当前点在当前生成树上到起点的简单路径上经过的点数

如果恰好是只有其中一项限制，我们都可以直接套最小生成树的模版改一改即可

1. 只有起点限制，我们可以暴力枚举起点然后套Prim即可 $O(n^3)$
2. 只有当前生成树的状态限制，我们可以额外开一个数组，记录加入生成树的点到起点经过的点数，然后dfs $O(2^{2n})$

然而本题这两个参数都要考虑，就不能直接套模版来改了（不优化的话，时间复杂度要到 $O(n2^{2n})$ ）

因此我们不妨采用 爆搜优化 -> 记忆化搜索 -> 动态规划 来解决该问题

我们把当前 生成树 的状态作为 DP 的阶段，那么需要额外记录的参数就是树的 深度

记录深度之后，可以保证我们枚举下一个阶段的状态时，能够轻易的计算他到起点的路径经过的点数

即我们把起点作为树的 root 然后一层一层构造 生成树

闫氏DP分析法

状态表示—集合$f_{i,j}:$ 当前生成树的状态是$i$ ($i$ 采用二进制压缩存储)，且树的深度为 $j$ 的方案
状态表示—属性$f_{i,j}:$ 该方案构成的生成树，费用最少$Min$
状态计算—$f_{i,j}:$
$$ f_{i,j} = \min (f_{pre,j-1} + j \times cost) $$

初始状态： $f_{i,0} \quad (0\le i \lt n)$
目标状态： $f_{1\cdots1,j} \quad (0\le j \lt n)$

其中，$pre$ 是枚举的所有树 $i$ 的子集，$cost$ 则是由 $pre$ 扩展一层后变成 $i$ 所用的所有边的边权之和

需要注意⚠️：这里枚举 $pre$首先必须满足一定能够由 $pre$ 自身的点向外扩散一层后能够变成状态 $i$

这算是一个简单的状态转移优化，因为如果所有状态都枚举的话，时间复杂度会退化成爆搜

可能有人看到该 DP分析 第一时间会有疑问（至少我有）：

在第 $j-1$ 到第 $j$ 层扩展的时候，有没有可能发生一次 $k-1$ 向 $k$ 层的扩展 (其中 $k < j$)

就是深层向下扩展时，出现了一个浅层往下延伸一个点的情况

根据我们的 转移方程，会把那个浅层扩展的路径数按照当前树的深度来计算，使得该方案费用比实际更大

这种方案是实际存在的，而且也是可能成为本题最优解答案的，但是我们可以不用考虑

为什么？因为该最优解方案是可以映射到我们DP方案中的某一个方案上的

我举一个简单的例子：

$$ f(0001_b,0) \rightarrow f(0011_b, 1) \rightarrow f(1111_b, 2) $$

其中点 $1$ 是通过 $1$ 层的点 $3$ 延伸到第 $2$ 层的，而点 $2$ 是通过起点 $4$ 延伸到第 $1$ 层的

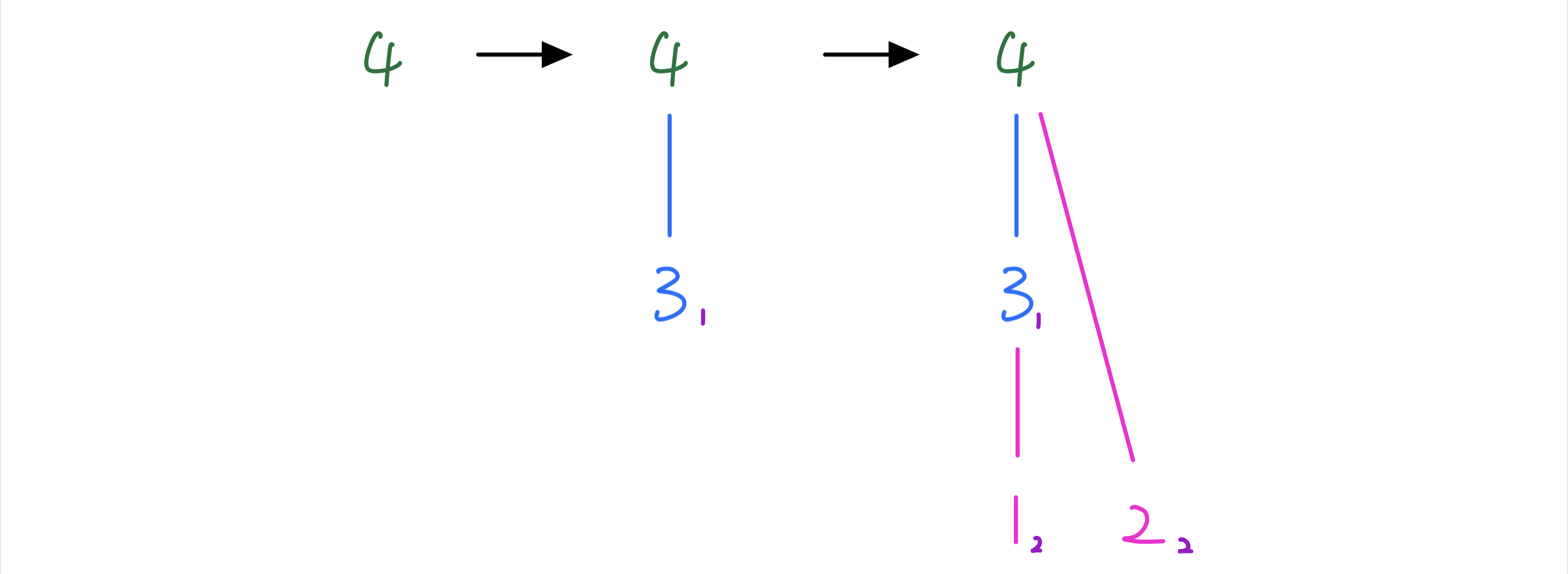
则该类方案都一一映射到下面这类方案下

$$ f(0001_b,0) \rightarrow f(0111_b, 1) \rightarrow f(1111_b, 2) $$

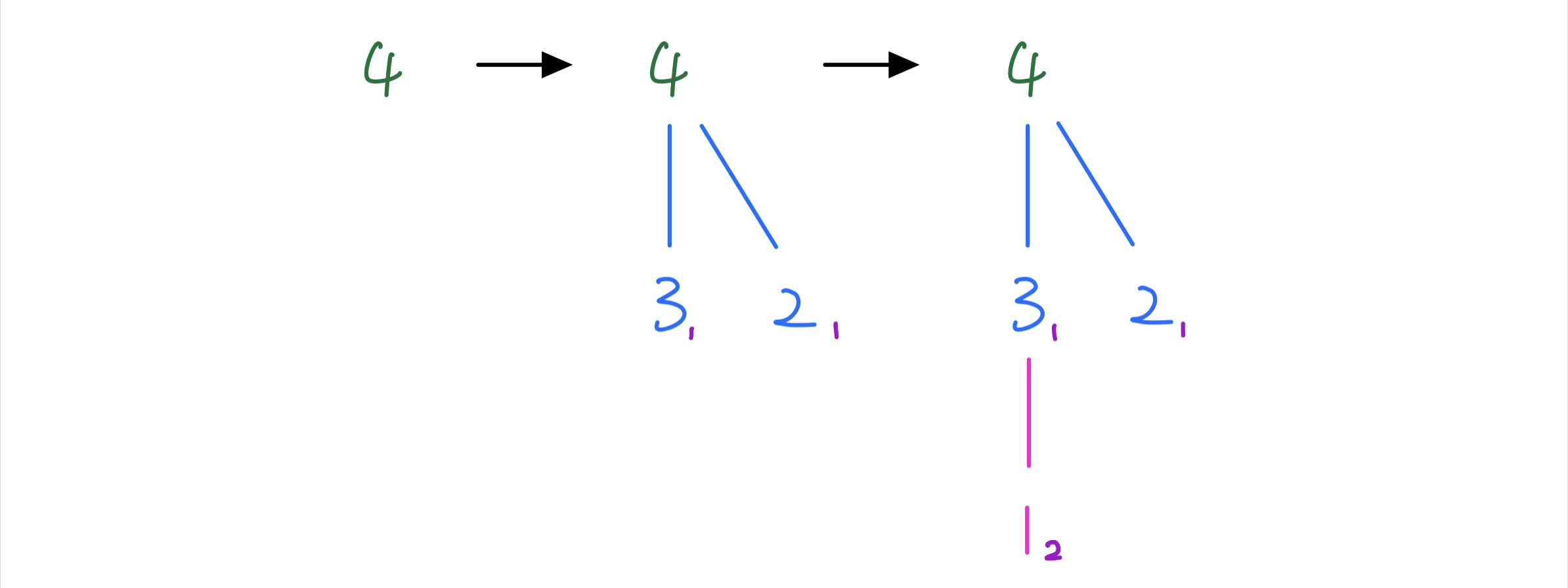
也就证明了我们该类DP方案的最终答案可以是最优解

Code

时间复杂度：

1. 预处理 $O(2^n \times n^2)$
2. 动态规划 $O(n^2 3^n)$ 借鉴 y总的分析

#include <iostream>
#include <cstring>

using namespace std;

const int N = 15, M = 1 << N, K = 1010;
const int INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int ne[M];
int f[M][K];

void init()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    for (int i = 0; i < n; ++ i) g[i][i] = 0;
    while (m -- )
    {
        int a, b, c;
        cin >> a >> b >> c;
        a --, b -- ;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    for (int st = 1; st < 1 << n; ++ st)//预处理所有状态能够扩展一层后得到的最大的下一层状态
        for (int i = 0; i < n; ++ i)
            if (st >> i & 1)
                for (int j = 0; j < n; ++ j)
                    if (g[i][j] != INF)
                        ne[st] |= 1 << j;
}
int get_cost(int cur, int pre)
{
    if ((ne[pre] & cur) != cur) return -1;//如果pre延伸不到cur直接剪枝
    int remain = pre ^ cur;//待更新的方案
    int cost = 0;//记录边权总和
    for (int i = 0; i < n; ++ i)
    {
        if (remain >> i & 1)
        {
            int t = INF;//找出当前连通块内能把该点加入所用的最小边的边长
            for (int j = 0; j < n; ++ j)
                if (pre >> j & 1)
                    t = min(t, g[j][i]);
            cost += t;
        }
    }
    return cost;//返回该次扩展的费用
}
//dp
int dp()
{
    memset(f, 0x3f, sizeof f);
    for (int i = 0; i < n; ++ i) f[1 << i][0] = 0;//开局免费选一个起点（初始状态）
    for (int cur = 1, cost; cur < 1 << n; ++ cur)
        for (int pre = cur - 1 & cur; pre; pre = pre - 1 & cur)
            if (~(cost = get_cost(cur, pre)))
                for (int k = 1; k < n; ++ k)
                    f[cur][k] = min(f[cur][k], f[pre][k - 1] + cost * k);
    int res = INF;
    for (int k = 0; k < n; ++ k) res = min(res, f[(1 << n) - 1][k]);//目标状态中找最优解
    return res;
}
int main()
{
    init();
    cout << dp() << endl;
    return 0;
}