算法分析

• 1、将每个区间按左端点从小到大进行排序

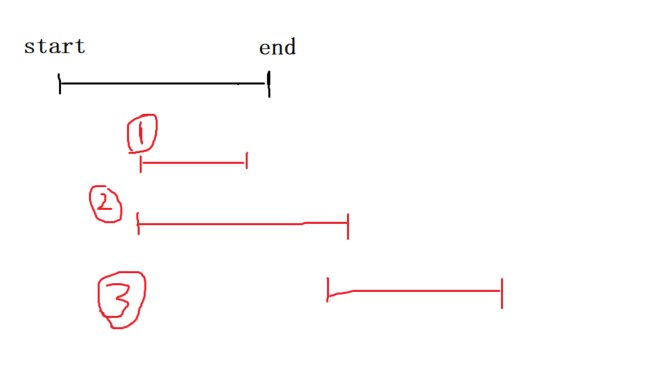
• 2、如图所示，可分3种情况

  • 情况一：当前区间完全被上一区间覆盖，直接跳过
  • 情况二：将当前区间的右端点更新为上一区间的右端点，达到区间延长的效果
  • 情况三：当前区间的左端点严格大于上一区间的右端点，则表示该区间不能合并，更新区间且count++

时间复杂度 $O(nlogn)$

Java 代码

import java.util.*;


public class Main{

    public static void main(String[] args) {
        List<PIIs> list = new ArrayList<PIIs>();
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        for(int i = 0;i < n;i++)
        {
            int L = scan.nextInt();
            int R = scan.nextInt();
            list.add(new PIIs(L,R));
        }
        //按左端点进行排序
        Collections.sort(list);
        int count = 0;
        int start = Integer.MIN_VALUE;
        int end = Integer.MIN_VALUE;
        for(PIIs item : list)
        {

            if(item.getFirst() > end)
            {
                count ++;
                start = item.getFirst();
                end = item.getSecond();
            }
            else
            {
                end = Math.max(end, item.getSecond());
            }
        }
        System.out.println(count);
    }

}



class PIIs implements Comparable<PIIs>{
    private int first;
    private int second;

    public int getFirst()
    {
        return this.first;
    }
    public int getSecond()
    {
        return this.second;
    }
    public PIIs(int first,int second)
    {
        this.first = first;
        this.second = second;
    }

    @Override
    public int compareTo(PIIs o) {
        // TODO 自动生成的方法存根
        return Integer.compare(first, o.first);
    }
}