ysDP

算法思路

ysDP
状态表示
    dp[i]
    集合:以第i只奶牛为结尾的所有合法选择方案的集合
    属性:max
状态划分
    没有选择第i只奶牛:
        等价于以第i-1只牛为结尾的最大值, dp[i-1]
    选择第i只奶牛:
        以包含i的连续区间长度为划分依据, 设长度为x, 1<=x<=m

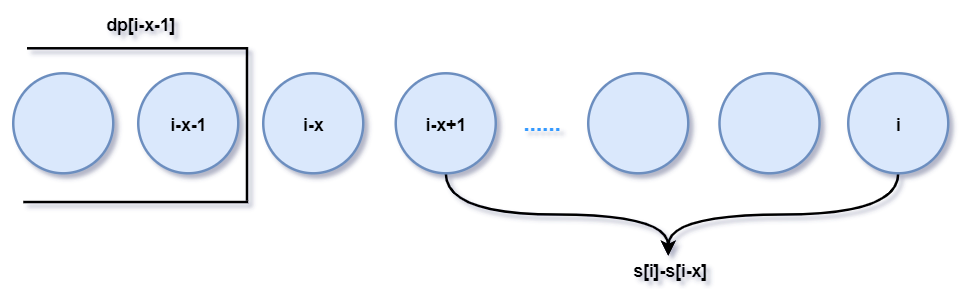
    dp[i] = max(dp[i-x-1]+s[i]-s[i-x]), s[]为前缀和数组,s[i]固定 --> 
    dp[i] = s[i] + max(dp[i-x-1]-s[i-x])
    令g[j] = dp[j-1] - s[j], dp[i] = s[i] + max(g[j]) i-m<=j<i
    对于每个dp[i]需要求一端区间的g的极值, 单调队列优化.

C++ 代码

#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

int n, m;
int q[N];
ll  s[N], dp[N];

ll g(int i)
{
    if( !i )
        return 0; //g[0] = 0 边界情况
    return dp[i-1] - s[i];
}

int main()
{
    scanf("%d%d",&n,&m);
    for( int i = 1; i <= n; i++ )   scanf("%d",&s[i]), s[i] += s[i-1];
    int tt = -1, hh = 0;
    q[++tt] = 0; //push 0 作为 g(0) 下标
    for( int i = 1; i <= n; i++ )
    {
        if( q[hh] < i - m ) hh ++ ;
        dp[i] = max( dp[i-1], s[i] + g(q[hh]) );
        while( hh <= tt && g(i) >= g(q[tt]) )   tt -- ;
        q[++tt] = i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}