算法

(染色问题、乘法原理) $O(n)$

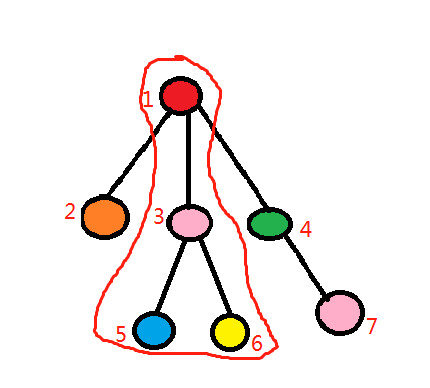
画圈的部分的染色方案数为 $_{K-2}P_2$
我们只需统计每个点与它的父节点以及孩子节点组成的团的染色数，然后利用乘法原理将它们相乘即可。
记每个点的孩子节点的个数为 $C_i$
对于根节点来说，它没有父节点，需要给自己和其孩子节点染色，由它和其孩子节点构成的团的染色方案数就是 $_K{P_{{C_1} + 1}}$
对于其他节点来说，自己和父节点颜色已经固定，只需给孩子节点染色，由它和其孩子节点构成的团的染色方案数就是 $_{K - 2}{P_{{C_i}}}$

C++ 代码

#include <bits/stdc++.h>
#include <atcoder/all>
using namespace atcoder;
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;

using mint = modint1000000007;

struct combination {
    vector<mint> fact, ifact; 
    combination(int n): fact(n + 1), ifact(n + 1) {
        fact[0] = 1;
        for (int i = 1; i <= n; ++i) fact[i] = fact[i - 1] * i;
        ifact[n] = fact[n].inv();
        for (int i = n; i >= 1; --i) ifact[i - 1] = ifact[i] * i; 
    }
    mint operator()(int n, int k) {
        if (k < 0 || k > n) return 0;
        return fact[n] * ifact[k] * ifact[n - k];
    }
} comb(100005);

mint f(int n, int k) {
    if (n < 0) return 0;
    // nPk = nCk * k!;
    mint res = comb(n, k);
    res *= comb.fact[k];
    return res;
}

int k;
mint ans;
vector<int> to[100005];
void dfs(int v, int p = -1) {
    for (int u : to[v]) {
        if (u == p) continue;
        dfs(u, v);
    }
    int nk = (p == -1) ? k : k - 2;
    int c = (p == -1) ? to[v].size() + 1 : to[v].size() - 1;
    ans *= f(nk, c);
}

int main() {
    int n;
    cin >> n >> k;

    rep(i, n - 1) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[a].push_back(b);
        to[b].push_back(a);
    }

    ans = 1;
    dfs(0);
    cout << ans.val() << '\n';

    return 0;
}