IDA*模板题

算法

（IDA*） O($560^{4}$)

先考虑每一步的决策数量：
当抽取长度为 ii 的一段时，有 $ n−i+1 $ 种抽法，对于每种抽法，有 $ n−i $ 种放法。另外，将某一段向前移动，等价于将跳过的那段向后移动，因此每种移动方式被算了两遍，所以每个状态总共的分支数量是：$∑ni=1(n−i)∗(n−i+1)/2 = (15∗14+14∗13+…+2∗1)/2=560$。

考虑在四步以内解决，所以最多有 $560^{4}$ 个状态，会超时。

因此我们用IDA*来解决此题。

本题的估价函数

• 估价函数需要满足：不大于实际步数
• 在最终状态下，每本书后面的书的编号应该比当前书多1。
• 每次移动最多会断开三个相连的位置，再重新加入三个相连的位置，因此最多会将3个错误的连接修正，所以如果当前有 $tot$ 个连接，那么最少需要 $⌈tot/3$⌉ 次操作。
• 因此当前状态 ss 的估价函数可以设计成 $f(s)=⌈tot/3]$。

如果当前层数加上 f(s)f(s) 大于迭代加深的层数上限，则直接从当前分支回溯。

并且由题目可知，答案的深度较浅，所以可以使用迭代加深的方式来求解

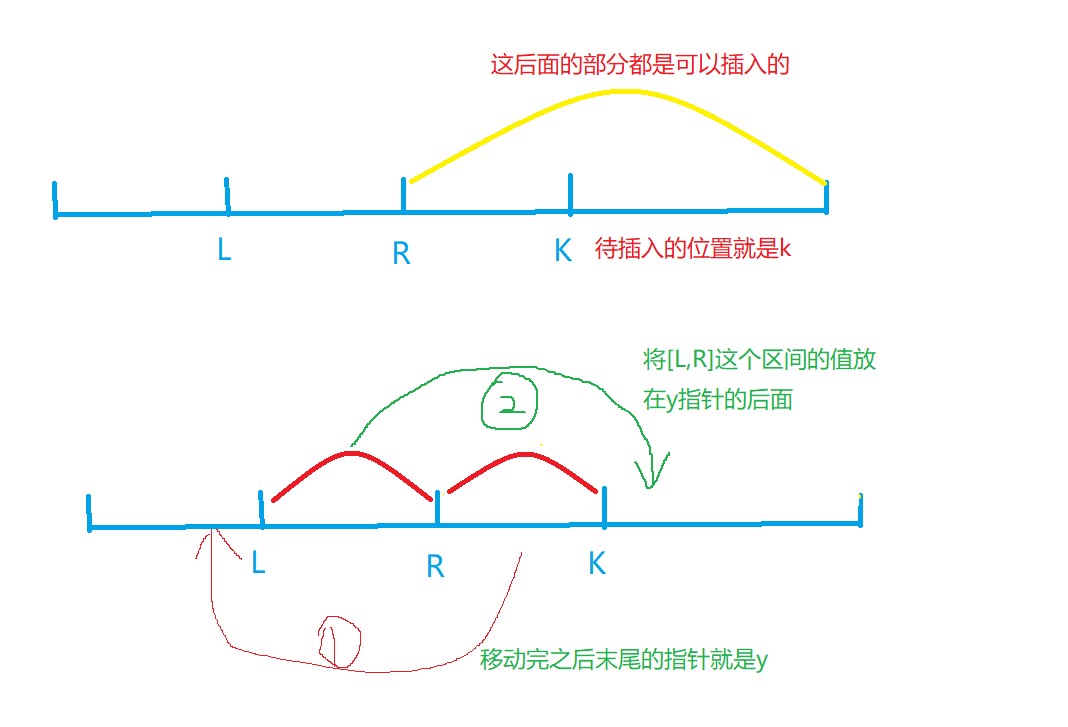
区间的移动步骤

IDA*

c++代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 16;
int q[N];   //存储初始序列
int w[5][N]; //w[i]表示第i次操作时的序列是什么
int n;

//估价函数：
int f(){  //本题的估价函数时计算有多少个不符合要求的后缀点()

    int total = 0;
    for(int i = 0;i < n - 1;++i){
        if(q[i] != q[i + 1] - 1) total ++;
    }
    return (total + 2) / 3;
}


bool dfs(int u,int max_depth){  //u表示当前的层数，max_depth表示最大的层数

    if(f() + u > max_depth) return false; 

    if(f() == 0) return true; //表示当前已经是顺序了

    //枚举抽取的区间长度
    for(int len = 1;len <= n;++len){
        //枚举当前区间的左端点
        for(int l = 0;l + len - 1 < n;++l){

            int r = l + len - 1;

            //枚举当前区间可以插入的位置:（[r + 1 ~ n - 1]）
            for(int k = r + 1;k < n;++k){

                //先记录当前状态，用于等下恢复现场
                memcpy(w[u],q,sizeof q);

                int y = l;
                //移动[R + 1,K]的部分
                for(int x = r + 1;x <= k;++x,++y) q[y] = w[u][x];
                //移动[L,R]的部分
                for(int x = l;x <= r;++x,++y) q[y] = w[u][x]; 

                if(dfs(u + 1,max_depth)) return true;

                //恢复现场
                memcpy(q,w[u],sizeof q);
            }
        }
    }
    return false;
}


int main(){
    int t;
    cin >> t;
    while(t--){
        cin >> n;
        for(int i = 0;i < n;++i) cin >> q[i];

        int depth = 0;
        while (depth < 5 && !dfs(0, depth)) depth ++ ;

        if(depth >= 5) puts("5 or more");
        else cout << depth << endl;
    }
    return 0;
}

同样的用A*算法也能够完成，但是时间慢了接近200ms左右，

总结了一下应该在何时选择 A∗ 或 IDA∗：

需要最小字典序时，状态表示很大，指数增长较快时，使用IDA∗
若状态容易表示，指数增长较慢时，使用A∗A∗（注意需要最小字典序时不能用A∗，因为他不是按照顺序搜索的）

A*

c++代码

//使用A*
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<unordered_set>
using namespace std;
typedef unsigned long long ULL;
const int N = 16;
int n;

struct state{
    int v[N],step,f;    //v[]表示当前的序列，step表示当前的步数，f表示当前状态的估计值 + 真实值

    //按照估价值 + 真实值进行从大到小排序  
    bool operator < (const state& x) const{
        return f > x.f;
    }
}start;

int f(state x){
    int res = 0;
    for(int i = 1; i < n; i++)
        if(x.v[i] - 1 != x.v[i - 1]) res++;
    return res % 3 ? res / 3 + 1 : res / 3;
}



ULL get(state x){   //得到state所代表的十进制数
    ULL res = 0;
    for(int i = 0;i < n;++i){
        res += res * 10 + x.v[i];
    }
    return res;
}

bool check(int v[]){  //判断是否已经到达了目标状态
    for(int i = 0;i < n;++i){
        if(v[i] != i + 1) return false; 
    }
    return true;
}


unordered_set<ULL> st;  //记录状态是否已经被记录过了
int Astart(){

    priority_queue<state> que;
    start.f = f(start) + 0;   //起点的步数为0
    que.push(start);
    st.insert(get(start));

    while(que.size()){

        state t = que.top();
        que.pop();
        if(t.f >= 5) return 5;  //直接判断f不用判断step，更快的剪枝

        if(check(t.v)) return t.step;


        //接下来就是枚举序列变化的过程了
        for(int len = 1;len <= n;++len){  //枚举长度

            for(int l = 0;l + len - 1 < n;++l){  //枚举当前区间的左端点
                int r = l + len - 1;

                for(int k = r + 1;k < n;++k){  //枚举可以插入的位置

                    state cur;  //用cur来记录更新的状态
                    for(int i = 0;i < n;++i) cur.v[i] = t.v[i];
                    int y = l;
                    for(int x = r + 1;x <= k;++x,++y){  
                        cur.v[y] = t.v[x];
                    }
                    for(int x = l;x <= r;++x,++y){
                        cur.v[y] = t.v[x];
                    }

                    if(st.count(get(cur)) > 0) continue;

                    st.insert(get(cur));
                    cur.step = t.step + 1;
                    cur.f = f(cur) + cur.step;   
                    que.push(cur);
                }
            }
        }

    }
}


int main(){
    int t;
    cin >> t;
    while(t--){
        cin >> n;
        st.clear();   //每次记得把st清空
        for(int i = 0;i < n;++i) cin >> start.v[i];

        int t = Astart();

        if(t >= 5) cout << "5 or more" << endl;
        else cout << t << endl;
    }

    return 0;
}