小国王

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

输入格式

共一行，包含两个整数 n 和 k。

输出格式

共一行，表示方案总数，若不能够放置则输出0。

数据范围

1≤n≤10,
0≤k≤n2

输入样例：

3 2

输出样例：

16

参考解释

https://www.acwing.com/solution/content/42890/

图解

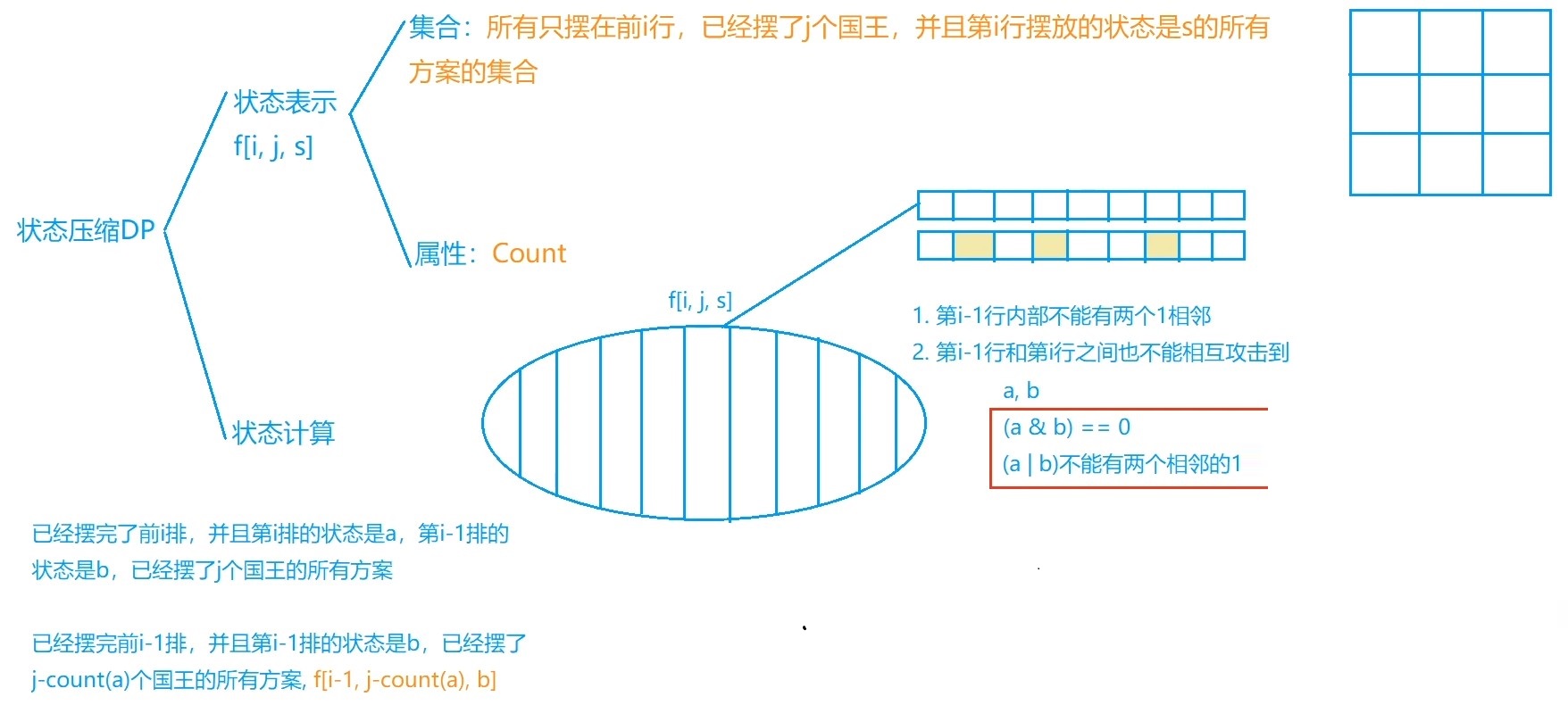
AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>

using namespace std;
using LL = long long;

const int N = 12, M = 1 << 10, K = 110;

int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
LL f[N][K][M];

bool check(int state)
{
    for (int i = 0; i < n; i ++)
        if ((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}

int count(int state)
{
    int res = 0;
    for (int i = 0; i < n; i ++) res += state >> i & 1;
    return res;
}

int main()
{
    cin >> n >> m;

    for (int i = 0; i < 1 << n; i ++)
        if (check(i))
        {
            state.push_back(i);
            cnt[i] = count(i);
        }

    for (int i = 0; i < state.size(); i ++)
        for (int j = 0; j < state.size(); j ++)
        {
            int a = state[i], b = state[j];
            if ((a & b) == 0 && check(a | b))
                head[i].push_back(j);
        }

    f[0][0][0] = 1;
    for (int i = 1; i <= n + 1; i ++)
        for (int j = 0; j <= m; j ++)
            for (int a = 0; a < state.size(); a ++)
                for (int b : head[a])
                {
                    int c = cnt[state[a]];
                    if (j >= c)
                        f[i][j][a] += f[i - 1][j - c][b];
                }

    cout << f[n + 1][m][0] << endl;

    return 0;
}