题目描述

给你一棵 n 个节点的有根树，节点编号从 0 到 n - 1。每个节点的编号表示这个节点的 独一无二的基因值（也就是说节点 x 的基因值为 x）。两个基因值的 基因差 是两者的 异或和。给你整数数组 parents，其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根，那么 parents[x] == -1。

给你查询数组 queries，其中 queries[i] = [node_i, val_i]。对于查询 i，请你找到 val_i 和 p_i 的 最大基因差，其中 p_i 是节点 node_i 到根之间的任意节点（包含 node_i 和根节点）。更正式的，你想要最大化 val_i XOR p_i。

请你返回数组 ans，其中 ans[i] 是第 i 个查询的答案。

样例

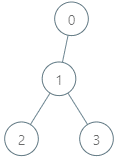
输入：parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]]
输出：[2,3,7]
解释：查询数组处理如下：
- [0,2]：最大基因差的对应节点为 0，基因差为 2 XOR 0 = 2。
- [3,2]：最大基因差的对应节点为 1，基因差为 2 XOR 1 = 3。
- [2,5]：最大基因差的对应节点为 2，基因差为 5 XOR 2 = 7。

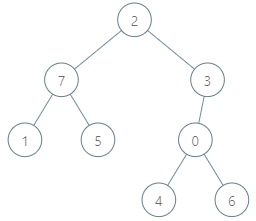
输入：parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]]
输出：[6,14,7]
解释：查询数组处理如下：
- [4,6]：最大基因差的对应节点为 0，基因差为 6 XOR 0 = 6。
- [1,15]：最大基因差的对应节点为 1，基因差为 15 XOR 1 = 14。
- [0,5]：最大基因差的对应节点为 2，基因差为 5 XOR 2 = 7。

限制

• 2 <= parents.length <= 10^5
• 对于每个 不是 根节点的 i，有 0 <= parents[i] <= parents.length - 1。
• parents[root] == -1
• 1 <= queries.length <= 3 * 10^4
• 0 <= node_i <= parents.length - 1
• 0 <= val_i <= 2 * 10^5

算法1

(可持久化字典树) $O((n + q) \log V)$

1. 如果查询一个数字，在一个集合中的异或最大值，则只需要将这个集合建立一棵 01 字典树，然后从根开始与待查询数字做逆向匹配。
2. 但如果是对多个集合查询，则需要每个集合都建立一棵字典树。
3. 在题目的场景下，如果每个节点都有一棵从当前节点到根节点的所有数字组成的字典树，则每次查询只需要 $O(\log V)$ 的时间（其中 $V$ 是最大可能的数字）。
4. 如果暴力构造，则时空复杂度都是 $O(n^2 \log V)$，不可接受。但由于这是一棵树，可复用的内容很多，所以考虑使用持久化的构造方法。
5. 对于有向边 $(x, y)$，假设 $x$ 的字典树已经创建好，则创建 $y$ 的字典树时，只需要从根节点新增一条 $y$ 的路径，不在 $y$ 路径上的分支直接指向 $x$ 上对应的节点，具体可以参考代码。
6. 这样每个点都只需要 $O(\log V)$ 的时间就可以新构造一棵树。

时间复杂度

• 建图需要 $O(n)$ 的时间
• 所有的点建树需要 $O(n \log V)$ 的时间。
• 每次查询需要 $O(\log V)$ 的时间。
• 故总时间复杂度为 $O((n + q) \log V)$。

空间复杂度

• 需要 $O(n \log V + q)$ 的空间存储图，所有的字典树，递归的系统栈以及答案。

C++ 代码

const int N = 100010;
const int M = 20 * N;

struct Node {
    bool valid;
    int nxt[2];
    Node() {
        valid = false;
        nxt[0] = nxt[1] = -1;
    }
};

class Solution {
private:
    Node node[M];
    int cnt;

    vector<int> graph[N];
    int h[N];

    void dfs(int u, int f) {
        int r = cnt++;

        int p = r;
        for (int d = 17; d >= 0; d--) {
            int b = (u >> d) & 1;
            node[p].nxt[b^1] = node[f].nxt[b^1]; // 节点复用

            node[p].nxt[b] = cnt++; // 新建节点
            p = node[p].nxt[b];
            node[p].valid = true;

            f = node[f].nxt[b];
        }

        h[u] = r;

        for (int v : graph[u])
            dfs(v, r);
    }

public:
    vector<int> maxGeneticDifference(vector<int>& parents,
    vector<vector<int>>& queries) {
        cnt = 0;
        int r = cnt++;
        node[r].nxt[0] = node[r].nxt[1] = r;

        const int n = parents.size();

        int u = -1;
        for (int i = 0; i < n; i++)
            if (parents[i] == -1) u = i;
            else graph[parents[i]].push_back(i);

        dfs(u, r);

        vector<int> ans(queries.size());
        for (int i = 0; i < queries.size(); i++) {
            int p = h[queries[i][0]];
            int v = queries[i][1];

            for (int d = 17; d >= 0; d--) {
                int b = (v >> d) & 1;

                if (node[node[p].nxt[b^1]].valid) { // 逆向匹配
                    ans[i] |= 1 << d;
                    p = node[p].nxt[b^1];
                } else {
                    p = node[p].nxt[b];
                }
            }
        }

        return ans;
    }
};

算法2

(离线，字典树) $O((n + q) \log V)$

1. 将询问离线，将每个询问放到树上对应的节点上。
2. 深度优先遍历整棵树，动态维护从根节点到当前节点路径的字典树，并处理所有当前节点对应的询问。
3. 动态维护包括新增一个节点和删除一个节点。

时间复杂度

• 预处理需要 $O(n + q)$ 的时间
• 每次动态维护字典树都需要 $O(\log V)$ 的时间，每次查询需要 $O(\log V)$ 的时间。
• 故总时间复杂度为 $O((n + q) \log V)$。

空间复杂度

• 需要 $O(n + q + V)$ 的空间存储图，字典树，递归的系统栈和答案。

C++ 代码

const int N = 100010;
const int M = (1 << 18) + 10;

struct Node {
    int counter, nxt[2];
    Node() {
        counter = 0;
        nxt[0] = nxt[1] = -1;
    }
};

class Solution {
private:
    Node node[M];
    int cnt;

    vector<int> graph[N];
    vector<pair<int, int>> q[N];
    int rt;

    vector<int> ans;

    void insert(int x) {
        int p = rt;

        for (int d = 17; d >= 0; d--) {
            int b = (x >> d) & 1;
            if (node[p].nxt[b] == -1) node[p].nxt[b] = cnt++;
            p = node[p].nxt[b];
            node[p].counter++;
        }
    }

    void remove(int x) {
        int p = rt;

        for (int d = 17; d >= 0; d--) {
            int b = (x >> d) & 1;
            p = node[p].nxt[b];
            node[p].counter--;
        }
    }

    int query(int x) {
        int p = rt;
        int res = 0;

        for (int d = 17; d >= 0; d--) {
            int b = (x >> d) & 1;
            if (node[p].nxt[b^1] != -1 && node[node[p].nxt[b^1]].counter > 0) {
                res |= 1 << d;
                p = node[p].nxt[b^1];
            } else {
                p = node[p].nxt[b];
            }
        }

        return res;
    }

    void dfs(int u) {
        insert(u);

        for (const auto &v: q[u])
            ans[v.second] = query(v.first);

        for (int v : graph[u])
            dfs(v);

        remove(u);
    }

public:
    vector<int> maxGeneticDifference(vector<int>& parents,
    vector<vector<int>>& queries) {
        cnt = 0;
        const int n = parents.size();

        int u = -1;
        for (int i = 0; i < n; i++)
            if (parents[i] == -1) u = i;
            else graph[parents[i]].push_back(i);

        for (int i = 0; i < queries.size(); i++)
            q[queries[i][0]].emplace_back(queries[i][1], i);

        ans.resize(queries.size());
        rt = cnt++;
        dfs(u);

        return ans;
    }
};