题目描述

OIER 公司是一家大型专业化软件公司，有着数以万计的员工。作为一名出纳员，我的任务之一便是统计每位员工的工资。这本来是一份不错的工作，但是令人郁闷的是，我们的老板反复无常，经常调整员工的工资。如果他心情好，就可能把每位员工的工资加上一个相同的量。反之，如果心情不好，就可能把他们的工资扣除一个相同的量。我真不知道除了调工资他还做什么其它事情。工资的频繁调整很让员工反感，尤其是集体扣除工资的时候，一旦某位员工发现自己的工资已经低于了合同规定的工资下界，他就会立刻气愤地离开公司，并且再也不会回来了。每位员工的工资下界都是统一规定的。每当一个人离开公司，我就要从电脑中把他的工资档案删去，同样，每当公司招聘了一位新员工，我就得为他新建一个工资档案。老板经常到我这边来询问工资情况，他并不问具体某位员工的工资情况，而是问现在工资第k多的员工拿多少工资。
每当这时，我就不得不对数万个员工进行一次漫长的排序，然后告诉他答案。
好了，现在你已经对我的工作了解不少了。正如你猜的那样，我想请你编一个工资统计程序。
怎么样，不是很困难吧？

样例

略

算法1

往上走两步两步一走，争取走后树更平

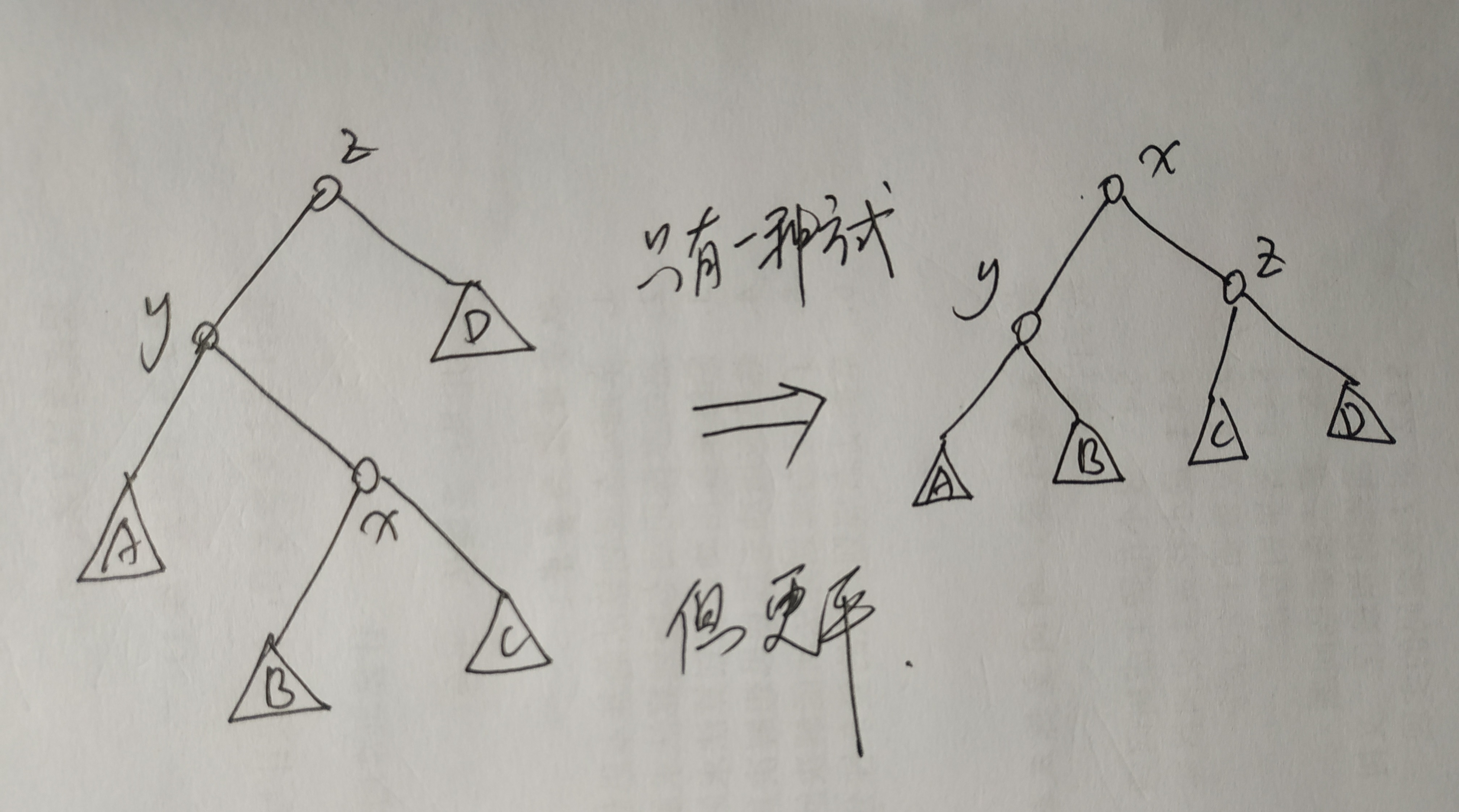
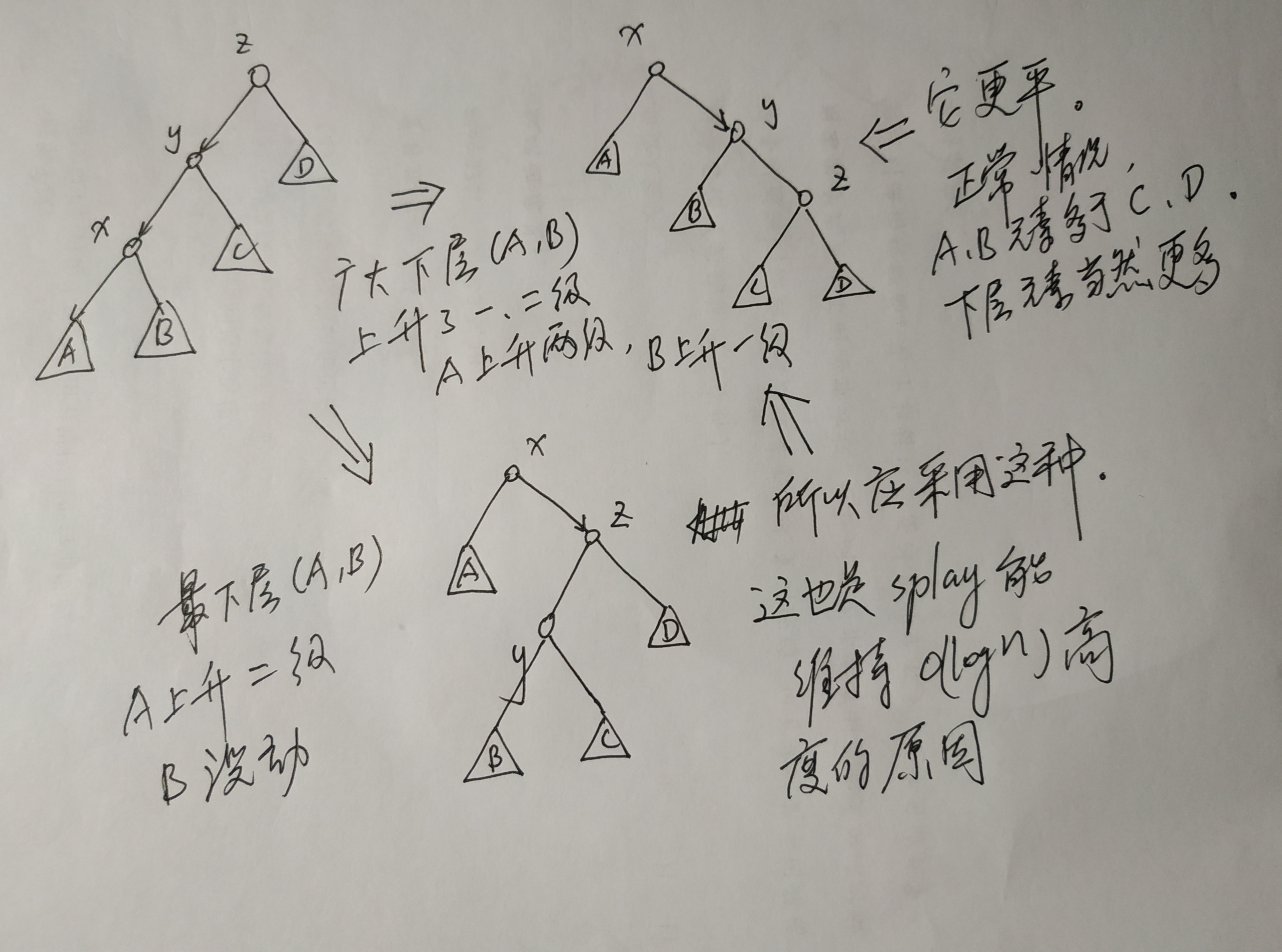
x上升时选择的方案，要尽量带上它的下属（子树）一起上升，这样更符合splay的初衷：访问局部化

解读请看代码

C++ 代码

#include <bits/stdc++.h>
using namespace std;

const int N=100010,inf=1e9;

int n,m,delta;
struct Node{
    int s[2],p,v,sz; //s:son,p:parent,v:value,sz:size
    void init(int _v,int _p){
        v=_v, p=_p, sz=1;
    }
    int &ls=s[0],&rs=s[1]; //ls: left son, rs:right son
} tr[N]; //tr: tree
int root,idx;

void collect(int x){
    tr[x].sz=tr[tr[x].ls].sz+tr[tr[x].rs].sz+1;
}

void rise(int x){ //把x向上升一下,官升一级
    int bs=tr[x].p, gb=tr[bs].p; //bs:boss, gb: grand-boss
    int k=(tr[bs].rs==x), kk=(tr[gb].rs==bs);
    tr[gb].s[kk]=x, tr[x].p=gb; //x替换bs，与gb建立关系
    tr[bs].s[k]=tr[x].s[k^1], tr[tr[x].s[k^1]].p=bs; //调整x的下属与bs的关系, 
    tr[x].s[k^1]=bs, tr[bs].p=x;  //调整x与bs的关系
    collect(bs),collect(x); //收集各自下属的信息，老bs要先做，对不起了
}

void splay(int x,int k){ //x越级做k的下属
    while(tr[x].p != k){ //两级两级往前跳
        int bs=tr[x].p, gb=tr[bs].p;
        if(gb != k)
            if( (tr[bs].rs==x) ^ (tr[gb].rs==bs) )  //不是线性，自己先跳，
                rise(x);    //以后老板和大老板都是自己直接下属，关系更平
            else rise(bs); //三级关系呈线性，老板带着自己跳，争取上下级关系更平
        rise(x); //自己再跳，前面的跳要分条件，是为了关系更平，即树更平，有利于搜索
    }
    if(!k) root=x; //自己是最大的老板
} 

int insert(int v){ //进入一个新员工，v是它的级别，左子小于父，右子大于父
                    //级别不是老板与下属的关系,级别类似于职称，上下关系是职务
                   //因此级别调整，不影响树的关系，也就是树不是靠v来维持的，但初始可以
    int x=root, p=0; //p:parent, x: 询问的当前点， pa--->x
    while(x)p=x, x=tr[x].s[v>tr[x].v]; //大于就放左，小于等于放右
    x=++idx; //新开点下标
    if(p) tr[p].s[v>tr[p].v]=x; //与父节点建立联系
    tr[x].init(v,p);
    splay(x,0); //这不是调整级别，只是部门
    return x;
}

int get(int v){
    int x=root,res;
    while(x){
        if(tr[x].v >= v) res=x, x=tr[x].ls;
        else x=tr[x].rs;
    }
    return res;
}

int kth(int k){
    for(int x=root;x;){ //从根开始,循环查找
        if(tr[tr[x].ls].sz >= k) x=tr[x].ls; //转到左
        else if( tr[tr[x].ls].sz+1==k) return tr[x].v;
        else k-=tr[tr[x].ls].sz+1, x=tr[x].rs; //转到右
    }
    return -1;  //没找到
}

int main(){
    cin>>n>>m;
    int L=insert(-inf), R=insert(inf);

    int tot=0;
    while(n--){
        char op[2];
        int k;
        scanf("%s%d",op,&k);
        if(op[0]=='I'){
            if(k>=m) k-=delta, insert(k), tot++;
        } else if(op[0]=='A') delta+=k;
        else if(op[0]=='S') {
            delta-=k;
            R=get(m-delta);
            splay(R,0), splay(L,R);
            tr[L].rs=0;
            collect(L), collect(R);
        } else {
            if(tr[root].sz - 2 < k) puts("-1");
            else printf("%d\n",kth(tr[root].sz-k)+delta);
        }
    }
    printf("%d\n",tot-(tr[root].sz-2));
}