算法

(容斥原理) $O(\log N)$

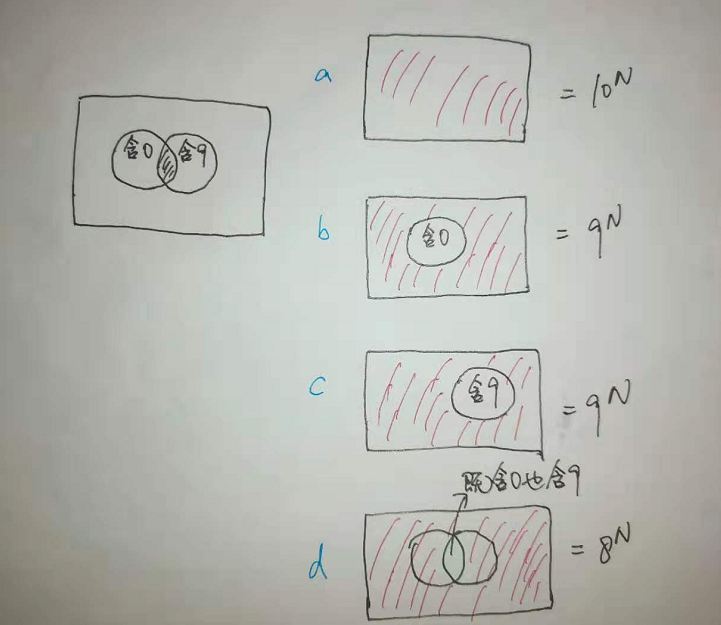
所以答案为 $a - b - c + d$

C++ 代码

#include <bits/stdc++.h>
#include <atcoder/all>
using namespace atcoder;

using std::cin;
using std::cout;

using mint = modint1000000007;

int main() {
    int n;
    cin >> n;

    mint a = mint(10).pow(n);
    mint b = mint(9).pow(n);
    mint c = b;
    mint d = mint(8).pow(n);

    mint ans = a - b - c + d;
    cout << ans.val() << '\n';

    return 0;
}

Python 代码

n = int(input())

mod = 10**9 + 7
ans = pow(10, n, mod)
ans -= pow(9, n, mod) * 2
ans += pow(8, n, mod)
print(ans%mod)