题目描述

给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。

Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。

输入格式
第一行输入整数 n。

接下来 n 行每行 n 个整数，其中第 i 行第 j 个整数表示点 i 到 j 的距离（记为 a[i,j]）。

对于任意的 x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。

输出格式
输出一个整数，表示最短 Hamilton 路径的长度。

数据范围
1≤n≤20
0≤a[i,j]≤107
输入样例：
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例：
18

时间复杂度

O(n^2*2^n)

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N=20,M=1<<N;

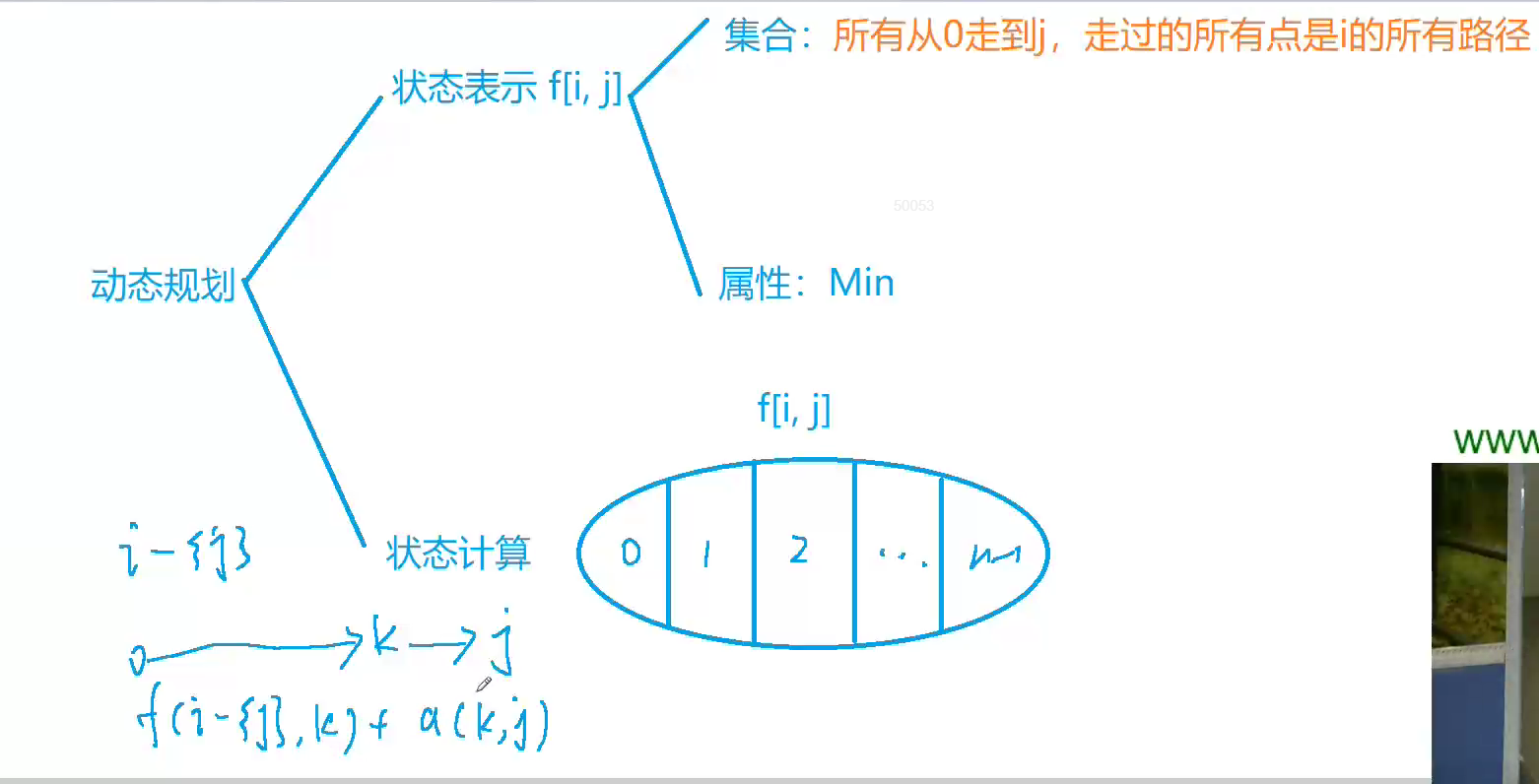
int f[M][N];   //f[i][j]表示从0走到j,走过的所有点是i的所有路径  例:i=110011(0代表没有走过,1代表走过,并且最右边的是0这个点)
int n;
int w[N][N];  //w[i][j]表示i到j这个点的距离

int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            scanf("%d",&w[i][j]);
        }
    }

    memset(f,0x3f,sizeof f);   //因为要求最短路径,初始化为正无穷
    f[1][0]=0;  //第一个点是不需要费用的

    for(int i=0;i<1<<n;i++){  //枚举点的所有状态
        for(int j=0;j<n;j++){   //枚举点的个数
            if(i>>j&1){  //i>>j:求i的第j位数字.  如果&1成立,则代表j这个点已经走过
                for(int k=0;k<n;k++){  //k->j
                    if(i>>k&1){   //跟上边的判断一样, 表示k这个点走过
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);  //判断本方案最优还是从i->k,再从k->j最优
                    }
                }
            }
        }
    }
    printf("%d",f[(1<<n)-1][n-1]);  //最优解
    return 0;
}