题意：给定$n$个数，表示$n$个人想要送礼物的目标，最终每个人只能送出一份礼物，每个人只能接受一份礼物，求出最多可以满足多少个人的要求，并输出最终赠送礼物的方案，此枚每个人不能把礼物送给自己。

分析：首先可以将$i$送礼物给$a[i]$，看成存在一条从$i$指向$a[i]$的边。不难看出最终能满足的人数为这$n$个数去重后数字的数量，因为这幅图的出度为$n$，而拥有入度的点不超过$n$，显然这些有入度的点最终都能得到入度。

如何构造一个合法的方案？

在建完图后，对于图中每个拥有入度的点，保留其中任意一条入度，删掉其余路径，那么这幅图最终会变成一个简单路径和环的集合，这时我们只需要将这些简单路径首尾相接即可。

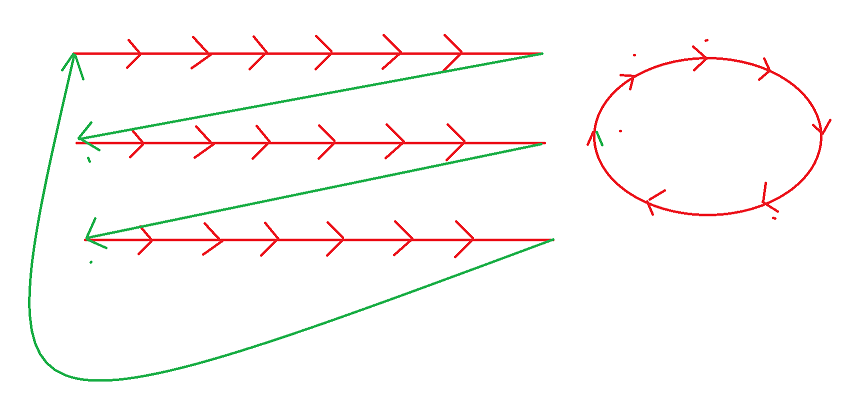
不过存在特殊情况，即存在孤立点：

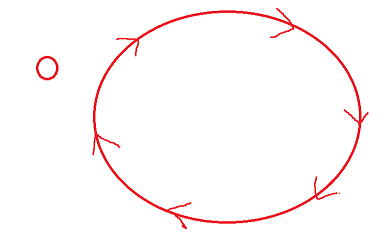
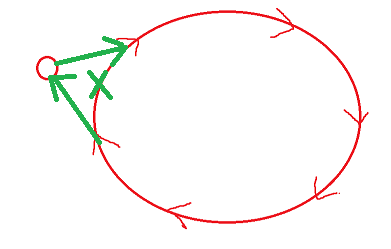
那么我们只需要先破环，再将孤立点并入环即可。
为了不使得答案减小，我们显然应该在孤立点希望赠送礼物的点(记为$x$)处破环，让$x$此时的收到礼物的赠送者指向孤立点，然后让孤立点指向$x$即可

#include <iostream>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <cmath>
#include <unordered_map>
#define bug1(g) cout<<"test: "<<g<<endl
#define bug2(g , i) cout<<"test: "<<g<<" "<<i<<endl
#define bug3(g , i , k) cout<<"test: "<<g<<" "<<i<<" "<<k<<endl
#define bug4(a , g , i , k) cout<<"test: "<<a<<" "<<g<<" "<<i<<" "<<k<<endl

#define INF 0x3f3f3f3f
#define fi first
#define se second
#define met(a , b) memset(a , b , sizeof a);
#define pb push_back

using namespace std;

typedef long long LL ;
typedef pair<int , int> PII;

const int N = 300010;

void solve()
{
    int n;
    cin >> n;
    int res = 0;
    vector<int> a(n), ne(n, -1), c(n, -1);
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        x--;
        a[i] = x;
        if (c[x] == -1)//如果还没人送给x
        {
            //i -> x
            c[x] = i;//送给x的人是i
            ne[i] = x;//i送给x
            res++;
        }
    }

    vector<int> head, tail;//找到每一条简单路径的头和尾
    for (int i = 0; i < n; i++)
        if (c[i] == -1) //如果第i个点没有入度，则从i出发就是一条简单路径
        {
            int j = i;
            while (ne[j] >= 0)//找到没有出度的点
                j = ne[j];

            //i就是这条简单路径的头，j是尾
            head.pb(i), tail.pb(j);
        }

    if (head.size())
    {
        if (head.size() == 1 && tail[0] == head[0]) //如果只有一个孤立点
        {
            //破环，让孤立点并入环中
            int x = head[0];
            int y = a[x];
            ne[c[y]] = x;//
            ne[x] = y;
        }
        else
            for (int i = 0; i < head.size(); i++) //让前一条路径的尾指向后一条路径的头，形成一条环路
                ne[tail[i]] = head[(i + 1) % head.size()];
    }

    cout << res << endl;
    for (int i = 0; i < n; i++)
        cout << ne[i] + 1 << ' ';
    cout << endl;
}

int main()
{
    freopen("in.txt", "r", stdin);
    int T = 1;
    cin >> T;
    for(int turn = 1 ; turn <= T ; turn++)
        solve();
}