算法

(贪心) $O(N\log N)$

结论：

考虑对于一个操作 $(a, c)$，如果当前的图有 $m$ 的连通分量，那么我们可以最优的连出 $m - \gcd(m. a)$ 条边，使得这 $m$ 个连通分量进一步变成 $\gcd(m, a)$ 个连通分量。

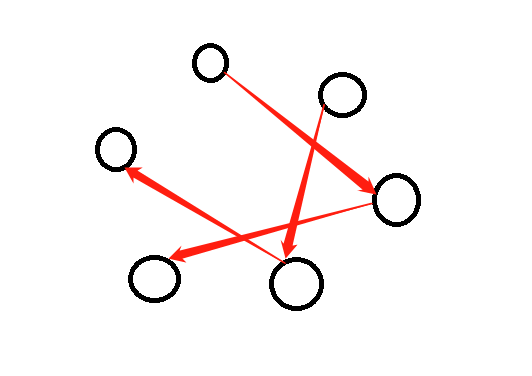
比如 $m = 6, a = 2$

为了满足总费用最小，所以在开始的时候要对所有操作按 $C$ 的大小进行升序排序。
然后按顺序依次加入适当的边，和 Kruskal 有些类似。

若最后的连通分量不为 $1$，表示这些操作不能让这些点连通。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define fi first
#define se second

using std::cin;
using std::cout;
using std::map;
using std::gcd;
using std::vector;
using ll = long long;
using P = std::pair<int, int>;

void chmin(ll& a, const ll b) { if (a > b) a = b; } 

int main() {
    int n, m;
    cin >> n >> m;

    vector<P> p(m);
    rep(i, m) cin >> p[i].se >> p[i].fi;

    sort(p.begin(), p.end());

    ll ans = 0;
    int mst = n; 
    rep(i, m) {
        int now = gcd(mst, p[i].se); // 当前的连通分量个数 
        ans += 1ll * (mst - now) * p[i].fi;
        mst = now;
    }

    if (mst != 1) puts("-1");
    else cout << ans << '\n';

    return 0;
}