算法

(二维前缀最小值) $O(HW)$

$ans = \min(A_{ij} + A_{i’j’} + (|i - i’| + |j - j’|) \cdot C)$

假设 $i \geqslant i’$ 且 $j \geqslant j’$，则有

$$ \begin{aligned} ans &= \min\large(A_{ij} + A_{i’j’} + (i - i’ + j - j’) \cdot C\large) \\\ &= \min\big(A_{ij} + A_{i’j’} + (i + j) \cdot C - (i’ + j’) \cdot C\big) \\\ &= \min\big((A_{ij} + (i + j) \cdot C) + ((A_{i’j’} - (i + j) \cdot C)\big) \\\ &= \min\big((A_{ij} + (i + j) \cdot C) + \min((A_{i’j’} - (i’ + j’) \cdot C)\big) \end{aligned} $$

记 $d_{ij} = \min((A_{i’j’} - (i’ + j’) \cdot C)$

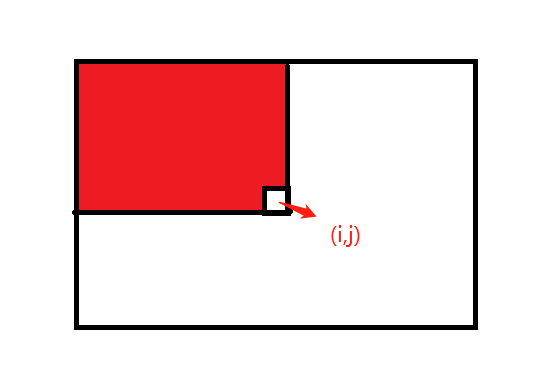
$d_{ij}$ 也就是红色区域内的所有点对 $(i, j)$ 这个点贡献的最小值，可以用类似二维前缀和的方法来处理。

而 $(i, j)$ 和 $(i’, j’)$ 这两点是对称的，所以还需要换个方向把上面的操作再做一遍即可。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::min;
using std::vector;
using ll = long long;

int main() {
    int h, w; ll c;
    cin >> h >> w >> c;

    vector a(h, vector<int>(w));
    rep(i, h)rep(j, w) cin >> a[i][j];

    const ll INF = 1e18;
    ll ans = INF;

    rep(_, 2) {
        vector d(h, vector<ll>(w, INF));
        rep(i, h)rep(j, w) {
            if (i) d[i][j] = min(d[i][j], d[i - 1][j]);
            if (j) d[i][j] = min(d[i][j], d[i][j - 1]);
            ans = min(ans, a[i][j] + (i + j) * c +  d[i][j]);
            d[i][j] = min(d[i][j], a[i][j] - (i + j) * c);
        }

        reverse(a.begin(), a.end());
    }

    cout << ans << '\n';

    return 0;
}