题目描述

对一个全为0数组的一部分下标插入一些值，并求出一段子区间上的所有数值的和，将和输出。

背模板时需要理清的思路

本题用离散化来做的原因是子区间上上有很多0，所以在遍历区间的时候跳过两个数间无用的0。C ++ 用vector来做离散化。
离散化对应下面①②③

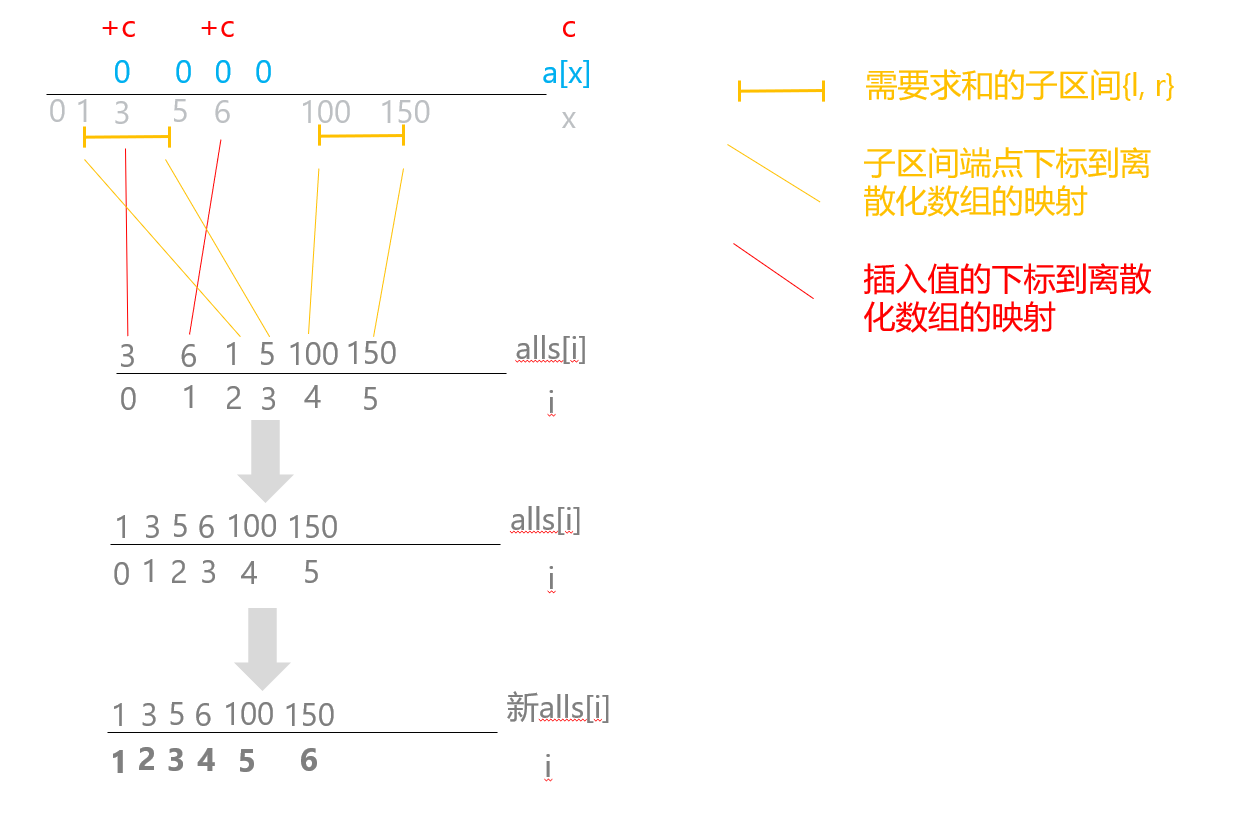
①第一步是将+c的非0值的下标放入到离散化数组alls中。（本题中all存的全是下标）
②第二步是将目标子区间的左右端点的下标放入到离散化数组alls中
③第三步是将离散化数组alls排序与去重。
④第四步是对需要+c的下标得值进行加值操作。这一步实现了两个内容，一个是将a[N]该加的加上了c，第二个是得到了“新”离散化数组。
⑤第五步是求子区间的和，在求和之前用的是a[alls.size()]来存入加值后的数组。

代码写法上的特点

①用vector来存离散化数组alls，本题的离散化数组的长度是300010
②本题中的pair的作用是存入对应下标和加值得二元组。二元组取得第一个值就是.first，取到第二个值就是.second。
③去重时用到unique函数，unique函数作用是将数组中不重复的元素放在最前面，将重复的元素放在最后面，返回的就是数组中不重复的最后一个数的下标。
④find函数作用是输入一个数，输出该数映射到”新”离散化数组中的下标，函数体用二分模板来处理（因为二分的模板最终会把区间缩到二分值的下标），返回r + 1的原因是离散化数组的下标是从0开始的，而接下来要处理的前缀和要从1开始存，使之变为”新”离散化数组（等价于上图输入a[N]，输出alls + 1）。
⑤本题中add和query中存的二元组，代表的意义是进行插入（加值）和查询操作。（x, c）前面x代表的是下标，后面c是下标对应的数要加c。
⑥a[N] s[N]的长度始终是和alls.size()对应着的。
⑦pair的初始化就是要先typedef定义，pair实例化就是用vector<pair对象名称> a, b
⑧unique函数本来在algorithm里面有，传的参数是alls.begin(),alls.end()。但本题是按y总的又定义了一遍，且传参数定义为一个即alls
⑨本题中erase掉的是alls中重复的元素，起点是alls中不重复元素的下一位下标，也就是unique函数中j ++最后一次执行完赋值并落在最后一个元素的下一位下标，即a.begin() + j不是最后一位不重复元素的下标，而是下一位的下标。
⑩i如果从0开始枚举而又要涉及到i - 1的操作时，判断语句可以写为(!i || a[i] != a[i - 1])

参考文献

参考y总的代码

C++ 代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;

vector<int> alls;
int n, m;
int a[N], s[N];
vector<PII> add, query;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;

    }
    return r + 1;
}


vector<int>::iterator unique(vector<int> &a)
{
    int j = 0;
    for (int i = 0; i < a.size(); i ++ )
        if (!i || a[i] != a[i - 1])
            a[j ++ ] = a[i];



    return a.begin() + j;
}

int main()
{
    cin >> n >> m;
    while (n -- )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        alls.push_back(x);

    }
    while (m -- )
    {
        int l, r, sum;
        cin >> l >> r;
        query.push_back({l, r});
        alls.push_back(l);
        alls.push_back(r);

    }

    sort(alls.begin(), alls.end());
    alls.erase(unique(alls), alls.end());

    for (auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    for (auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;

    }
    return 0;
}