算法

(主客転倒) $O(N\log N)$

记 $c_i$ 表示含有 $i$ 且 $i$ 是第二大的区间个数，于是 $ans = \sum c_i * i$

问题就转化成了如何求 $c_i$

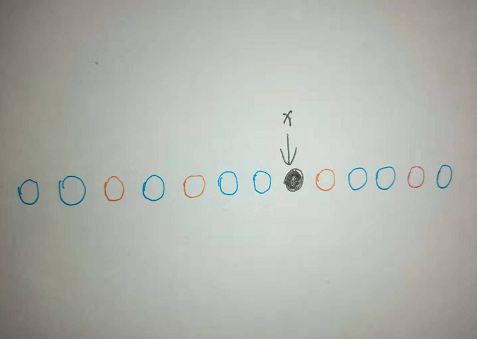
这里假设蓝圈 $\leqslant x$，红圈 $> x$，如果想让 $x$ 为第二大，那么只能让区间恰好包含一个红圈

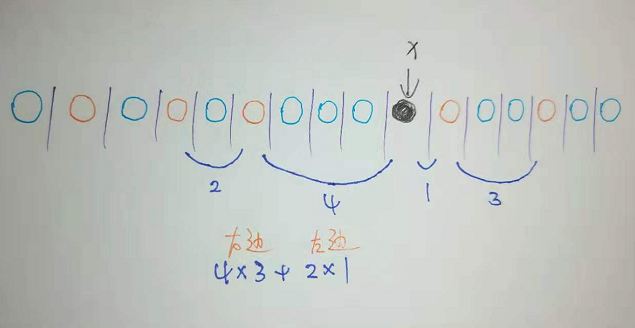
所以我们只需用 std::set 来找出每个 $x$ 对应的这四个变量即可。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::set;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];
    rep(i, n) a[i]--;

    vector<int> idx(n);
    rep(i, n) idx[a[i]] = i;

    set<int> s;
    ll ans = 0;
    for (int x = n - 1; x >= 0; --x) {
        int i = idx[x];
        ll c = 0;
        { // calc c
            s.insert(i);
            vector<int> l(2, -1);
            vector<int> r(2, n);
            { // calc l
                auto it = s.find(i);
                rep(j, 2) {
                    if (it == s.begin()) break;
                    --it;
                    l[j] = *it;
                }
            }
            { // calc r
                auto it = s.find(i);
                rep(j, 2) {
                    ++it;
                    if (it == s.end()) break;
                    r[j] = *it;
                }
            }
            vector<int> ls(2);
            ls[0] = i - l[0]; ls[1] = l[0] - l[1];
            vector<int> rs(2);
            rs[0] = r[0] - i; rs[1] = r[1] - r[0];
            c = (ll)ls[0] * rs[1] + (ll)ls[1] * rs[0];
        }
        ans += c * (x + 1);
    }

    cout << ans << '\n';

    return 0;
}