题目描述

给定一个 n∗n 的棋盘，以及一个开始位置和终点位置。

棋盘的横纵坐标范围都是 0∼n。

将一个国际象棋中的骑士放置在开始位置上，请问将它移动至终点位置至少需要走多少步。

一个骑士在棋盘上可行的移动方式如下图所示：

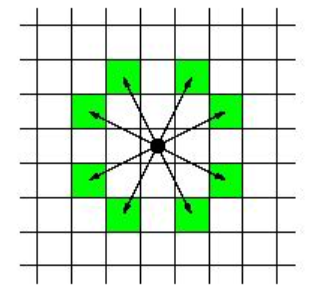
输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组测试数据第一行包含整数 n，表示棋盘大小。

第二行包含两个整数 x,y 用来表示骑士的开始位置坐标 (x,y)。

第三行包含两个整数 x,y 用来表示骑士的终点位置坐标 (x,y)。

输出格式

每组数据输出一个整数，表示骑士所需移动的最少步数，每个结果占一行。

数据范围

4≤n≤300,
0≤x,y≤n

输入样例：

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

输出样例

5
28
0

算法

使用广度优先遍历（宽搜BFS）就可以了。（宽搜函数体内部用队列来是实现#include<queue>）
小技巧：网格中的移动方向用向量组来表示，简化移动问题，便于解决问题。
举例表示：

int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

使用时：

int nowx = v1.front(), nowy = v2.front();

C++ 代码

#include<iostream>
#include<queue>
#include<cstring>

using namespace std;

const int N = 310;

int t, n, ax, ay, bx, by;
int q[N][N];
int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

void BFS(int x, int y)
{
    queue<int> v1, v2;
    v1.push(x);
    v2.push(y);
    while(!v1.empty())
    {
        int nowx = v1.front(), nowy = v2.front();
        v1.pop(), v2.pop();
        if(nowx != bx || nowy != by)
        {
            for(int i = 0; i < 8; i ++)
            {
                int cx = nowx + dx[i], cy = nowy + dy[i];
                if(cx >= 0&& cx < n&& cy >= 0&& cy < n&& !q[cx][cy])
                {
                    q[cx][cy] = q[nowx][nowy] + 1;
                    v1.push(cx);
                    v2.push(cy);
                }
            }
        }
        else
            return;
    }
}

int main()
{
    cin >> t;
    while(t --)
    {
        memset(q, 0, sizeof(q));
        cin >> n;
        n ++;
        cin >> ax >> ay;
        cin >> bx >> by;
        BFS(ax, ay);
        cout << q[bx][by] << endl;
    }
    return 0;
}