题目描述

对二维数组的子区域的所有值加c，重新输出这个数组

背模板时需要理清的思路

本题的差分数组是b[N][N]，因为需要在原数组中的子区间每一个数都要加c，所以要把原数组a[N][N]视为前缀和数组。

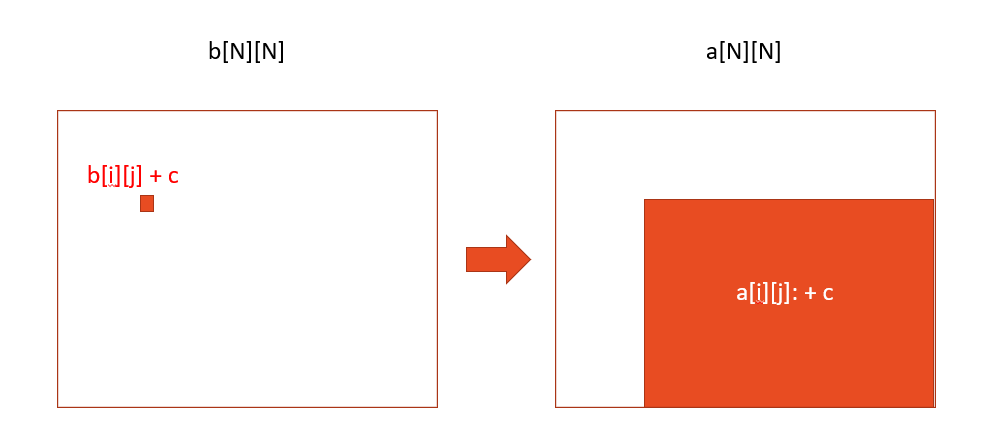
①（第一步是进行差分数组的存储）。存储的过程同样要用到insert()函数。insert()的函数体实现的差分数组加值过程b[i][j] += c可以想象为前缀和数组a[i][j]包含右下部分的所有值都会加c。，这个包东西的过程与求前缀和子区间包东西的想象过程是相反的。
②（第二步是恢复差分数组为前缀和数组），恢复的过程类似于对左上部分包东西的过程，公式b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]就是自身包东西来得到一个前缀和数组，与求前缀和子区间包东西的想象过程是相同的。

代码写法上的特点

①insert()函数在本题有两个作用，第一个时用来存储差分数组，可以用insert(i, j, i, j, a[i][j])来完成，原因是。第二个是用来做差分数组子区间上的加值计算，也就是insert(x1, y1, x2, y2, c)，即题意想实现的内容。

参考文献

参考y总的代码

C++ 代码

#include <iostream>

using namespace std;

const int N = 1e3 + 10;
int n, m, q;
int a[N][N], b[N][N];



void insert(int x1, int y1, int x2, int y2, int c) 
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -=c;
    b[x2 + 1][y2 + 1] += c;



}

int main()
{
    scanf("%d%d%d", &n, &m, &q );

    for (int i = 1; i <= n; i ++ )

        for (int j = 1; j <= m; j ++ )
            cin >> a[i][j];

    for (int i = 1; i <= n; i ++ )

        for (int j = 1; j <= m; j ++ )
                insert(i, j, i, j, a[i][j]);

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);

    }
    for (int i = 1; i <= n; i ++ ) 
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j]  + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
         for (int j = 1; j <= m; j ++ )

            printf("%d ", b[i][j]);

        puts("");
    } 

    return 0;

}