历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 327. 玉米田【线性状压DP+滚动数组优化+目标状态优化】原题链接简单

作者：

一只野生彩色铅笔 , 2021-07-14 23:37:01 , 所有人可见 , 阅读 5923

60

9

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个 $n \times m$ 的 $01$ 矩阵， $0$ 的位置不能放置棋子， $1$ 的位置能放置棋子

若在坐标 $(x,y)$ 放置了棋子，则 四相邻 的位置上不能放置棋子

求摆放的 方案数，答案对 $10^8$ 取模

分析

本题基本类似于上一题 AcWing 1064. 小国王【线性DP+状压DP+滚动数组优化+细节优化】

在本篇中没提及的内容，基本都在上一篇中详细分析了 【很详细!】

本题需要额外处理的，是给定的 $01$ 矩阵里存在着的不能放置棋子的位置

我们用二进制存储的状态 $state$ 中，使用 $1$ 表示在该位置放置棋子， $0$ 表示在该位置没有棋子

因此我们可以把矩阵每一层的状态也用二进制来压缩存储，且用 $0$ 表示该位置能放棋子， $1$ 表示不能放

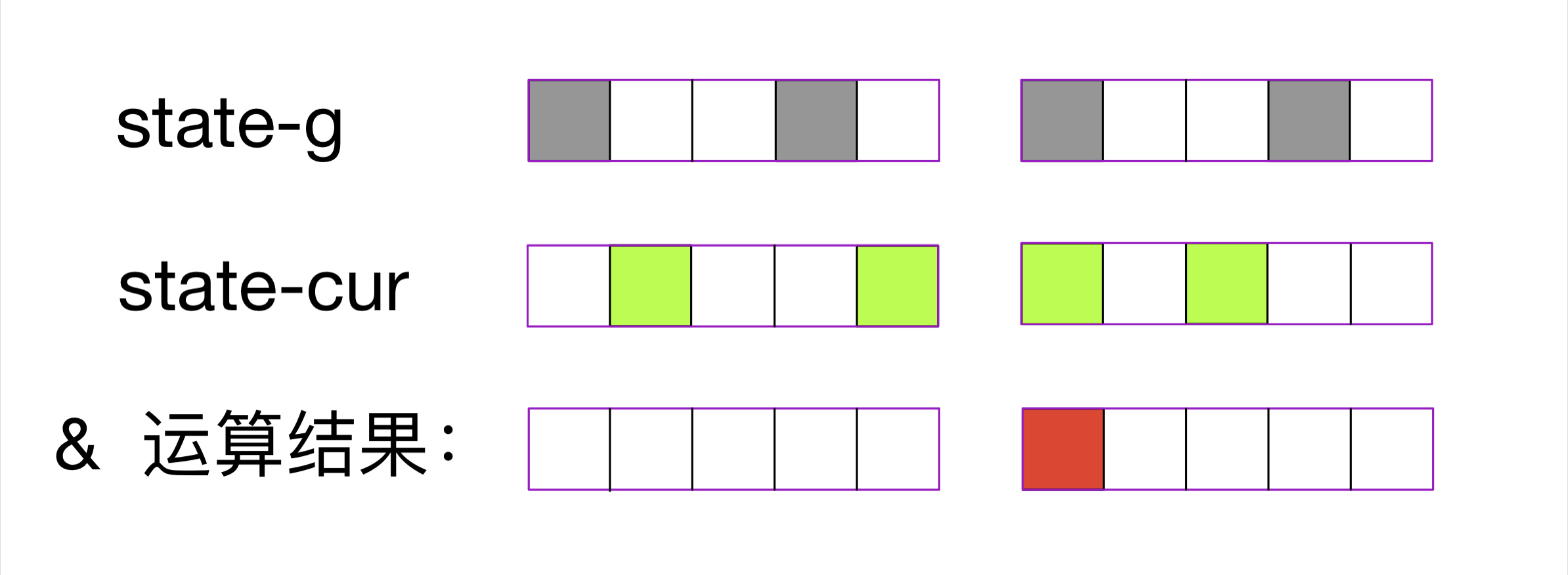
这样，只需把枚举的状态 $state_{cur}$ 与这一层的状态 $state_{g_i}$ 做 & 运算

结果为0，表示 放置棋子 的位置没有与 不能放置棋子 的位置重叠，则该状态合法
结果为1，表示 放置棋子 的位置与 不能放置棋子 的位置发生重叠，则该状态 不合法

具体如下图所示：

闫氏DP分析法

状态表示—集合 $f_{i,j}:$ 考虑前 $i$ 层，且第 $i$ 层状态是 $j$ 的方案
状态表示—属性 $f_{i,j}:$ 方案的总数 $Sum$
状态计算— $f_{i,j}:$
$f_{i,j} = \sum_{pre} f_{i-1,pre}$
其中 $pre$ 是枚举的能够与 $j$ 合法存在于相邻行中的所有状态

Code

这里用了 目标状态优化

有不理解的可以看 AcWing 1064. 小国王【线性DP+状压DP+滚动数组优化+细节优化】里的内容

#include <iostream>
#include <vector>

using namespace std;

const int N = 14, M = 1 << N, mod = 1e8;

int n, m, k;
int g[N];
int f[N][M];
vector<int> state;
vector<int> head[M];

bool check(int state)
{
    return  !(state & state << 1);
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j < m; ++ j)
            cin >> k, g[i] |= !k << j;
    for (int st = 0; st < 1 << m; ++ st)
        if (check(st))
            state.push_back(st);    //预处理合法状态
    for (auto st: state)
        for (auto ne_st: state)
            if (!(st & ne_st))
                head[st].push_back(ne_st);  //预处理合法状态的合法转移
    f[0][0] = 1;
    for (int i = 1; i <= n + 1; ++ i)
        for (auto st: state)
            if (!(st & g[i]))
                for (auto pre_st: head[st])
                    f[i][st] = (f[i][st] + f[i - 1][pre_st]) % mod;
    cout << f[n + 1][0] << endl;
    return 0;
}

滚动数组优化

同上一题思路一样，也可以用滚动数组优化

    f[0][0] = 1;
    for (int i = 1; i <= n + 1; ++ i)
        for (auto st: state)
        {
            f[i & 1][st] = 0;
            if (!(st & g[i]))
                for (auto pre_st: head[st])
                    f[i & 1][st] = (f[i & 1][st] + f[(i - 1) & 1][pre_st]) % mod;
        }
    cout << f[(n + 1) & 1][0] << endl;

34 评论

颓废 2023-04-06 10:16

###状态转移比较简单，不预处理也行

#include<bits/stdc++.h>

using namespace std;

const int N=14,M=1<<12,mod=1e8;
int n,m;
int g[N][N];
int f[N][M];
bool check(int i,int x)
{
    for(int j=m-1,k=0;j>=0;j--,k++)
       if((x>>j&1)==1&&g[i][k]==0)
           return false;
    return !(x&(x>>1));
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
       for(int j=0;j<m;j++)
           cin>>g[i][j];
    f[0][0]=1;

    for(int i=1;i<=n+1;i++)
       for(int j=0;j<1<<m;j++)
          for(int k=0;k<1<<m;k++)
          {
              if(!check(i,j)||!check(i-1,k)||(j&k)!=0) continue;
              f[i][j]=(f[i][j]+f[i-1][k])%mod;
          }
    printf("%d",f[n+1][0]);
    return 0;
}

Kusoul 2023-12-18 18:13

这个复杂度最坏好像高了10倍

jatro13 2022-08-27 20:01

g[i] |= !k << j 是什么意思？

Seeker. 2022-09-04 08:41

g[]数组是用来存储每一行土地状态的，你手动模拟一下，把g[]存的数值转换成2进制，就会发现，输入中是0的地方在g[]的二进制表示中变成了1，表示这块土地不能种植，输入中是1的地方在g[]的二进制表示中变成了0，表示这块土地可以种植，例如题中的输入样例，输入的时候是

1 1 1
0 1 0

那么在g[]数组里存储的就是（把g[]里的数值转换成2进制来表示哈）

0 0 0
1 0 1

自动AC姬 2022-11-24 21:39 回复了 Seeker. 的评论

对，就是对应位置的0-1互换了但观察一下代码，y总那个j是从0~m - 1，导致最后存到g[]里的状态其实是经过左右颠倒的，如果按照常规的0-1互换想法需要j从m - 1~0。

当然了，就算左右颠倒对结果其实是无影响的，因为在状态转移时选择的状态也是对应颠倒（可以想象就是把整个图也左右翻转了一遍）的。

._728 2023-01-05 09:58 回复了自动AC姬的评论

对对对我正在想这个图是颠倒的但发现并不影响

Chen_acwing_1024 2023-05-01 16:40 回复了自动AC姬的评论

厉害了

skymiles 12个月前回复了自动AC姬的评论

是的，其实就是应该m-1 ~ 0这么记录g数据

阳光男孩_7 10个月前

三篇都没说滚动数组啥意思…

秧歌star 2024-03-19 14:01

忘记了，不需要枚举玉米个数，答案无需要求玉米个数，只需要枚举方案和，并且对玉米个数无要求哎，写多了

秧歌star 2024-03-19 13:57

无优化代码
···
#include [HTML_REMOVED]
#include [HTML_REMOVED]
#include [HTML_REMOVED]
#include [HTML_REMOVED]

using namespace std;

const int N = 15, M = 1 << N,mod = 1e8;

int f[N][N * N][M];
int e[N][N],n,m,cnt[M];

vector[HTML_REMOVED] state;
vector[HTML_REMOVED] head[M];

bool check(int x)
{
for(int i = 0; i < m; i++)
if(x >> i & 1 && x >> (i + 1) & 1)
return false;
return true;
}

int find(int x)
{
int res = 0;
for(int i = 0; i < m; i)
if(x >> i & 1) res;
return res;
}

bool check2(int u,int state)
{
for(int i = 0; i < m; i++)
{
int j = state >> i & 1;
if(!e[u][i + 1] && j)
return false;
}

return true;

}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i)
for(int j = 1; j <= m; j) cin >> e[i][j];

for(int i = 0; i < 1 << m; i++)
    if(check(i))
    {
        cnt[i] = find(i);
        state.push_back(i);
        //cout << i << " " << cnt[i] << endl;
    }

for(int i = 0; i < state.size(); i++)
    for(int j = 0; j < state.size(); j++)
    {
        int a = state[i], b = state[j];
        if((a & b)== 0)
            head[a].push_back(b);
        // cout << a << "--- " <<  endl;
        // for(int k : head[a])
        //     cout << k << " " << endl;
    }

f[0][0][0] = 1;

for(int i = 1; i <= n + 1; i++)
    for(int j = 0; j <= n * m; j++)
        for(int k = 0; k < state.size(); k++)
        {
            int a = state[k];
            if(check2(i,a))
            {
                //cout << a << " " << endl;
                for(auto b : head[a])
                    if(check2(i - 1,b))
                    {
                        if(j >= cnt[a])
                        {
                            f[i][j][a] = (f[i][j][a] + f[i - 1][j - cnt[a]][b]) % mod;
                            //cout << f[i][j][a] << endl;
                        }
                    }
            }
        }

int res = 0;
for(int i = 0; i <= n * m; i++) res = (res + f[n+1][i][0]) % mod;

cout << res;

return 0;

}
···

kimihiki 2024-01-14 23:41

为什么只用判断g[i] & state[a] 而不用判断b的

Cloudddddd 9个月前

关于为什么只用判断g[i] & state[a] 而不用判断b的，这是因为b作为上一层的状态，已经被判断为false了，因此这个状态的方案数一直是0，因此是否判断b已经不重要了

污秽之翼 2023-10-17 13:24

check确实巧妙

wo怎么什么都不会 2022-05-17 13:44

大佬为什么只要判断第 i 行方案合法，为什么不判断第 i - 1行是否也合法

buuacm7 2022-05-18 09:39

我想是不是这样呢，当枚举到第i层状态时，i-1层状态已经枚举完了，就是说i-1层的满足 1该行不相连 2与第i行不相连 3只在肥沃的土地上种植才被赋予了值而不满足的被赋值为0 加了也没关系，所以不用判断第 i-1 行是否合法。

wo怎么什么都不会 2022-05-18 12:52 回复了 buuacm7 的评论

大佬的确是这样的，%%%%%

KobeBryant24 2022-04-08 22:00

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;
const int N = 13, M = 1<<N, MOD = 1e8;
int n, m;
int g[N];
int dp[N][M];
vector<int> state;
bool check(int x) {
    while(x) {
        if(x&1 && x>>1&1)
            return false;
        x >>= 1;
    }
    return true;
}
int main() {
    cin >> m >> n;
    for(int i = 1; i <= m; ++i) 
        for(int j = 0; j < n; ++j){
            int x;
            cin >> x;
            g[i] += (!x<<j);    
        }
    for(int i = 0; i < 1<<n; ++i) 
        if(check(i))
            state.push_back(i);

    dp[0][0] = 1;

    for(int i = 1; i <= m; ++i) {
        for(int j = 0; j < state.size(); ++j) {//i-1
            for(int k = 0; k < state.size(); ++k) {//i
                int a = state[j], b = state[k];
                if(a&b) continue;
                if(g[i]&b)  continue;
                dp[i][b] = (dp[i][b] + dp[i-1][a]) % MOD;
            }
        }
    }
    int ans = 0;
    for(int j = 0; j < state.size(); ++j) 
        ans = (ans + dp[m][state[j]]) % MOD;

    cout << ans << endl;
    return 0;
}

但是为什么我用滚动数组优化结果就错了呢

究极米缸 2022-05-10 17:10

同问

stamina_zeng 2022-10-17 22:46 回复了究极米缸的评论

不理解，不用head进行预处理，直接暴力，感觉这样写也没问题呀，不知道哪里的细节没有考虑好

stamina_zeng 2022-10-18 12:10

for(int i=1;i<=n+1;i)
{
for(int j=0;j<nums.size();j)
{
f[i&1][j]=0;
if(!(mp[i]&nums[j]))
for(int k=0;k<nums.size();k++)
{
int a=nums[j],b=nums[k];
if(a&b)continue;
f[i&1][j]=(f[i&1][j]+f[i-1&1][k])%p;
}
}
}
还有一个f[i&1][j]=0的初始化

包子云 2022-02-25 11:14

bool check(int state)
{
return !(state & state << 1);
}
楼主的check 时而左移，时而右移？？

acmdyh 2022-03-07 18:15

yiyang

包子云 2022-03-07 20:14 回复了 acmdyh 的评论

个人喜欢固定一种写法，养成习惯

用户名未被使用 2022-02-05 17:29

🌈✏️酱 yyds!

qbz666 2021-11-06 17:24

%%%

Link_Cut_Y 2021-10-01 20:09

#include <iostream>

using namespace std;

int main()
{
    cout << “dalao %%%”;
    return 0;
}

Morgannr 2022-03-22 18:50

引号错了

Link_Cut_Y 2022-03-23 08:48 回复了 Morgannr 的评论

abababab

Morgannr 2022-03-23 08:50 回复了 Link_Cut_Y 的评论

Link_Cut_Y 2021-10-01 20:07

%%% dalao tql !!

Peter_5 2021-09-05 18:09

巨巨的check函数好妙啊！

Vergissmeinnicht 2021-08-12 10:00

🌈✏️酱 yyds!

abc喵 2021-08-11 17:30

🌈✏️酱 yyds!

App 内打开

AcWing 327. 玉米田【线性状压DP+滚动数组优化+目标状态优化】 原题链接 简单

题目描述

分析

闫氏DP分析法

Code

34 评论

AcWing 327. 玉米田【线性状压DP+滚动数组优化+目标状态优化】原题链接简单