/*
1、理解hp与ph数组，以及为什么需要它们
* 堆h[i]只能存放数据，不能存放是第几个数字，所以需要ph[k] = i来指明，第k个数字在h[]中对应的i是多少
* 在执行交换操作的时候，可以直接交换数字,swap(h[a],h[b])
但是对于ph[k_1] = a和ph[k_2] = b来说，a和b是它们存放的值，不 能通过值来找下标，也就是找不k_1,k_2是多少
* 于是引入hp[a] = k_2，hp[b] = k_2，则可以实现反向的操作

2、形象理解heap_swap中的次序是任意的
h[]：房间号无直接实际意义，里边住着犯人
ph[]：花名册，狱警所有，写明了几号犯人住在哪个房间号里，用于抓某些人
（但是狱警无权过问每个号里住的是谁）
hp[]：住户册，监狱所有，写明了哪个房间号里住的是几号，用于管理监狱
（但是监狱没必要知道哪个犯人住在哪里）
heap_swap：已知两个犯人住的地方，交换它们住的地方，并且让狱警和管理 处都知道这件事情
swap(h[a], h[b])：两个人换地方住
swap(hp[a], hp[b])：监狱管理处翻房间号，把里边存放的犯人号交换
swap(ph[hp[a]], ph[hp[b]])：狱警：先申请查住户册，看这两个地方住的谁，再在花名册下写下来，这两个人位置换了
h[a] = 10, h[b] = 20 swap: h[a] = 20,h [b] = 10
hp[a] = 1 ,hp[b] = 2 swap:hp[a] = 2 ,hp[b] = 1
ph[1] = a ,ph[2] = b swap:ph[1] = b ,ph[2] = a
//这种不变形也很像线代中：代表交换的初等矩阵，进行逆运算之后，仍然是该初等矩阵

大佬解释的很清楚，终于明白了orz

orz

orz

orz

生动形象orz

牛！

orz

太强了（模拟堆这个图可以玩狱警/doge）

# 写的真好

orz

Orz

orz

Orz，大佬牛逼，写的太好了

orz

# orz

orz

Orz~

感谢，解释的真的很好

https://www.acwing.com/activity/content/code/content/6714238/
给大佬的讲解配了个例子

orz

orz

orz

orz

太牛逼了

h[1] = a ,ph[2] = b swap:ph[1] = b ,ph[2] = a
中 可以发现 直接是 ph[hp[a]] = b ph[hp[b]] = a 就行，不用调用swap函数， 毕竟 ph 数组存放的是 h 的下标, 用h 的下标 a,b 去间接交换 ph 数组中的值, 而 对应的 ph[hp[a]] 在没用交换函数时 值 就是a , 而ph[hp[b]] 为b ;
所以可以直接赋值来减少一次 函数的调用

h[x] 表示树中位置 x 的元素
ph[k] = x 表示第 k 个插入的元素在树中存放的位置 x
此时如果要交换 ph 中的两个元素需要知道树中位置 x 是第几个被插入的, 于是便引入了数组 hp
hp[x] = k 表示树中位置 x 存放的为第 k 个插入的元素

妙啊

orz

tql

#include <iostream>

using namespace std;

const int N = 1e5 + 10;
//h代表heap（堆），ph（point->heap）可以获得第几个插入的元素现在在堆的那个位置
//hp(heap->point)可以获得在堆的第n个元素存的是第几个插入的元素
//siz是大小
int h[N], ph[N], hp[N], siz;
int n, idx = 0; //idx-每个元素的插入次序

// 堆的全新的交换方式
void heap_swap(int a, int b)
{
    //先由hp找到对应的插入次序，然后交换ph数组中记录的两个元素的下标
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]); //交换hp数组中记录的两个元素的插入次序
    swap(h[a], h[b]); // 最后交换堆中的两个元素
}

void down(int u)
{
    int t = u; //让t代指u以及其两个儿子（三个点）中的最大值，先初始化为u
    if (u * 2 <= siz && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= siz && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u / 2] > h[u])
    {
        heap_swap(u, u / 2);
        u /= 2;
    }
}

int main()
{
    scanf("%d", &n);
    while (n--)
    {
        string op;
        int k, x;
        cin >> op;

        //插入一个数 x
        if (op == "I")
        {
            scanf("%d", &x);
            siz++;
            idx++;
            ph[idx] = siz; //堆尾插入，故第idx次插入的元素下标为siz
            hp[siz] = idx; //当前下标为siz的元素为第idx次插入
            h[siz] = x; //当前插入的值，即h[ph[idx]=x
            up(siz); //从堆尾向上调整
        }
        //输出当前集合中的最小值
        else if (op == "PM") printf("%d\n", h[1]);
        //删除当前集合中的最小值
        else if (op == "DM")
        {
            heap_swap(1, siz); //用堆尾元素覆盖头元素
            siz--;
            down(1);
        }
        //删除第 k 个插入的数
        else if (op == "D")
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, siz);
            siz--;
            down(k), up(k); //只会执行一个
        }
        //修改第 k 个插入的数，将其变为 x
        else if (op == "C")
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            down(k), up(k);
        }
    }

    return 0;

}

可以用multiset+unordered_map直接模拟，适合$Saber$

#include<bits/stdc++.h>
using namespace std;
multiset<int> q;
unordered_map<int,int> f;
int n,k,x,l;
string s;
int main(){
    ios::sync_with_stdio(0),cin>>n;
    for(int i=1;i<=n;++i){
        cin>>s;
        if(s=="I") cin>>x,f[++l]=x,q.insert(x);
        else if(s=="PM") cout<<*q.begin()<<"\n";
        else if(s=="DM") q.erase(q.begin());
        else if(s=="D") cin>>k,q.erase(q.find(f[k]));
        else cin>>k>>x,q.erase(q.find(f[k])),q.insert(f[k]=x);
    }
}

saber啥意思

AC Saber

# Or2

你屁股怎么能这么翘

ORZ

为什么vs2019用scanf会会报错

好像是微软觉得这个函数不安全，自己改成了scanf_s

可以加上这个宏定义#define _CRT_SECURE_NO_WARNINGS，就能用scanf了

加上这个确实可以，谢谢

删除操作里面， k = ph[idx]; //必须要保存当前被删除结点的下标，这一点非常重要，不然ph[idx]在交换操作后可能会发生变化，从而导致后续up, down的传入参数有问题

一、ph[] 和 hp[] 的含义
ph[k] = a: 第 k 个插入的数在堆中的下标是 a
hp[a] = k: 堆中下标是 a 的节点是第 k 个插入的数

二、为什么要引入 ph[] 和 hp[]?
AcWing 839. 模拟堆 和 AcWing 838. 堆排序最大的不同在于，需要记录第 k 个插入的数在堆中的位置，因而自然引出 ph[] 数组。

三、只引入 ph[] 为什么不行?
问题是交换节点 a 和 b，同时也需要交换节点 a 和 b 对应的 ph 值，即要找到 ph[i] = a 和 ph[j] = b，进行交换 swap(ph[i], ph[j])，这样就需要遍历 ph[]，时间复杂度高。
注意：ph[] 的有效下标一直到当前插入的数的个数，而非堆中的节点数目cnt，因此需要遍历的点更多，并且删除节点时，也必须删除该节点对应的 ph 值，否则会存在多个 ph[?] = a 的情况。

补充：
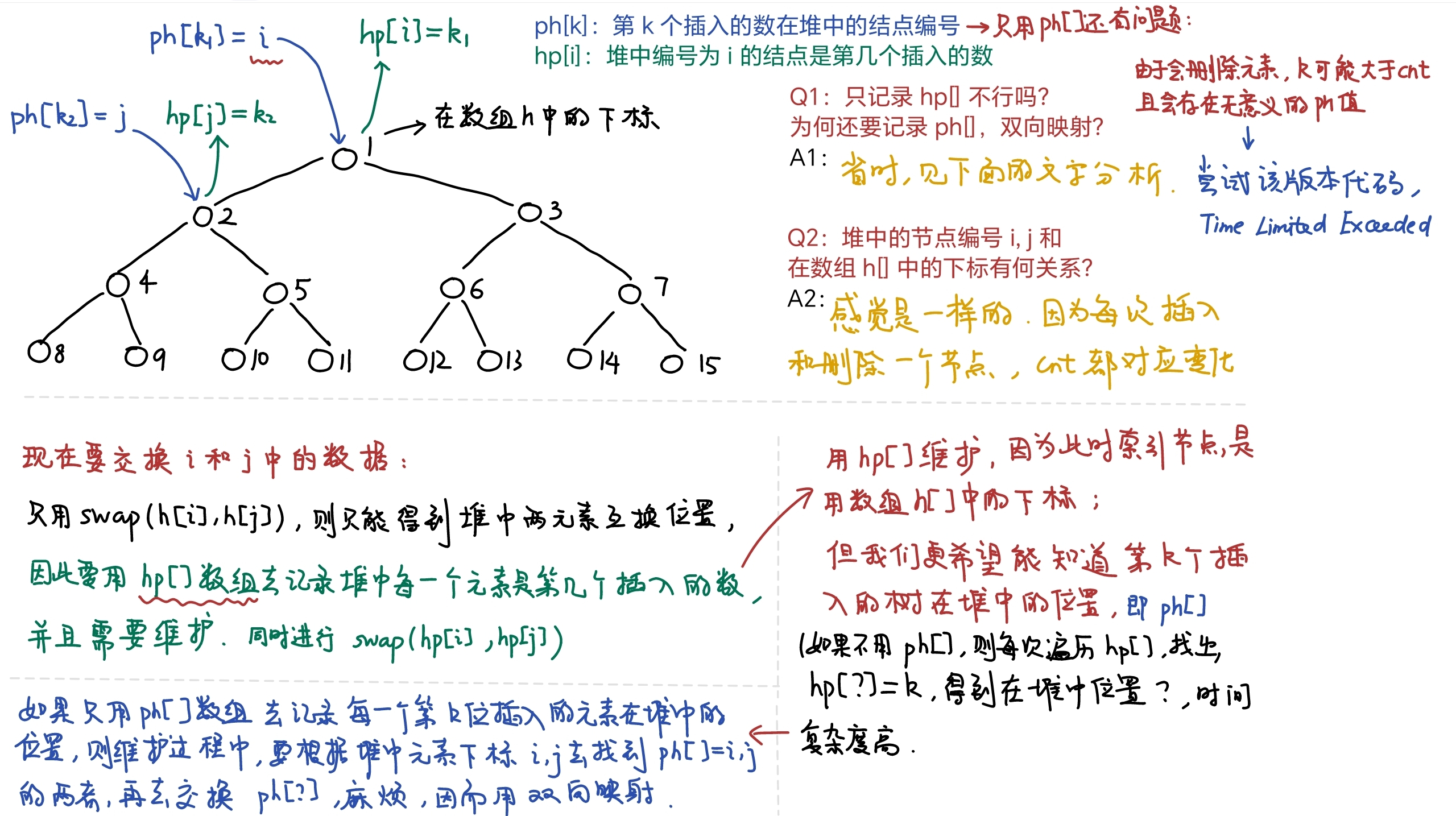
1、思路分析如下图

2、尝试模拟了只用 ph[] 的情况，出现 Time Limited Exceeded，
代码如下：

#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

const int N = 100010;

int h[N], cnt; // 用 size 不如用 cnt
int hp[N], ph[N]; // ph[k] 第 k 个插入的元素 在堆中的位置

void heap_swap(int a, int b)
{
    int i = 1, j = 1; // 记录结点 a 和 b 对应的 k 值（第几个插入的数）
    for(; i < N; i++){
        if(ph[i] == a) break;
    }
    for(; j < N; j++){
        if(ph[j] == b) break; 
    }
    swap(ph[i], ph[j]);
    swap(h[a], h[b]);
}

// 循环执行：在当前结点及其孩子节点中，选择最小值与当前节点交换
void down(int u)
{
    int t = u; // t 记录当前三者的最小值
    // 和左儿子比较
    if(u*2 <= cnt && h[u*2] < h[t]){
        t = u*2;
    }
    // 和右儿子比较
    if(u*2 + 1 <= cnt && h[u*2+1] < h[t]){
        t = u*2 + 1;
    }
    if(t != u){
        heap_swap(t, u);
        down(t);
    }
}

// 循环执行：如果比父节点小，则上移
void up(int u)
{
    while(u/2 && h[u/2] > h[u]){
        heap_swap(u/2, u);
        u = u/2;
    }
}

int main()
{
    int n, m = 0; // 记录是当前第几个插入的数

    scanf("%d", &n);

    while(n --){
        char op[5];
        int k, x;

        scanf("%s", op);
        if(!strcmp(op, "I")){ // strcmp 返回值：<0 表示 str1 < str2, =0 表示 str1 = str2, >0 表示 str1 > str2
            scanf("%d", &x);
            cnt ++;
            m ++;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt); // 没有采用数组建堆的O(n)方式，而是采用 插入到尾结点再 up() 调整 这一基本做法，时间复杂度更高
        }
        else if (!strcmp(op, "PM")){
            printf("%d\n", h[1]);
        }
        else if(!strcmp(op, "DM")){
            heap_swap(1, cnt);
            // 由于删除元素元素，结点 cnt 对应的 ph 无意义
            for(int i = 1; i < N; i++){
                if(ph[i] == cnt){
                    ph[i] = 0;
                    break;
                }
            }
            cnt --;
            down(1);
        }
        else if(!strcmp(op, "D")){
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, cnt);
            // 由于删除元素元素，结点 cnt 对应的 ph 无意义
            for(int i = 1; i < N; i++){
                if(ph[i] == cnt){
                    ph[i] = 0;
                    break;
                }
            }
            cnt --;
            down(k), up(k); // 至多只执行一个
        }
        else{
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            down(k), up(k);
        }
    }

    return 0;
}

其实理解完全没有那么难 更没有为此写一篇题解 建议好好学一下数据结构理论课 对学习算法有大帮助

有无推荐？

交换前ph[hp[a]]=a, ph[hp[b]]=b

else if(s==”D”){
cin>>x;

        heap_swap(ph[x],si);

        si--;

        down(ph[x]),up(ph[x]);


    }

为什么我这么写就会有问题呢？

orz

int ph[N], hp[N];
//ph[j] = k : 第j个插入点的下标是k； hp[k] = j : k下标表示的是第j个点插入的 其中k是下标！
//ph作用很大很显然，是用来在位置j上存储一个数，表示它是第k个输进程序的。在数组发生改变时，或直接要求更改第k个插入时，输入的是k、是ph[j]=k的右值，但是我要改变的不是k，是想把k的位置j和另一个位置i上的值交换位置，所以现在的情况是 只知道值k但是难以知道k对应的位置j，所以一个通过右值k找回下标的映射表hp[k] = j就应运而生了

讲的太好了，懂了！感谢

太通俗易懂了，orz

你好像写反了

每个结点所对应的 ph hp的值是一一对应的 双箭头。当交换两结点的值之后，ph和hp都需要分别进行一次交换才行

由于heap存的是 元素 存在down 和 up 会使得 元素的值对应的下标发生改变

从而找不到第k个插入元素对应的下标

这时候 使用 hp 来 映射第k个插入的元素对应下标

当heap发生swap时，hp也要发生swap 来交换第k个元素heap交换后对应新的下标

有了下标 还不能 交换值

所以要引入 ph 来 记录第k个元素对应新下标对应的新值（因为heap可能发生多次交换，hp对应的新下标可能发生多次改变，其每次交换之前的值必须记录下来，就引入了ph）

if (!strcmp(op, “D”))
{
scanf(“%d”, &k);
heap_swap(ph[k], cnt);
cnt – ;
up(ph[k]);
down(ph[k]);
}为什么不能这样，是因为ph有可能有特定的情况会被改变吗