1.举例说明区间合并的条件：

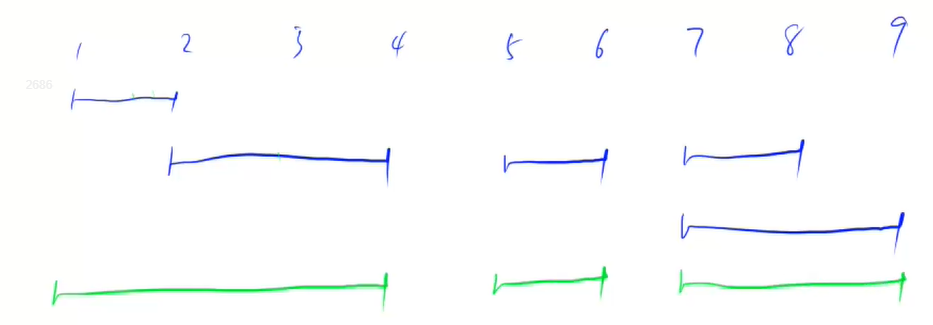
2.分为3种情况！

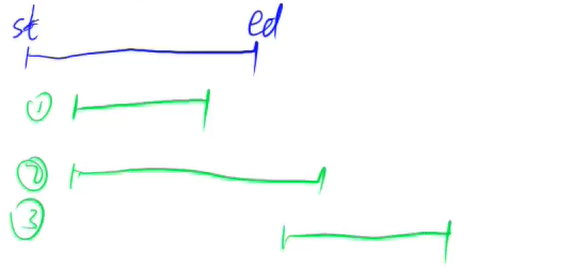
3.3种情况如何去合并区间：

4.如何确定合并后的区间个数：

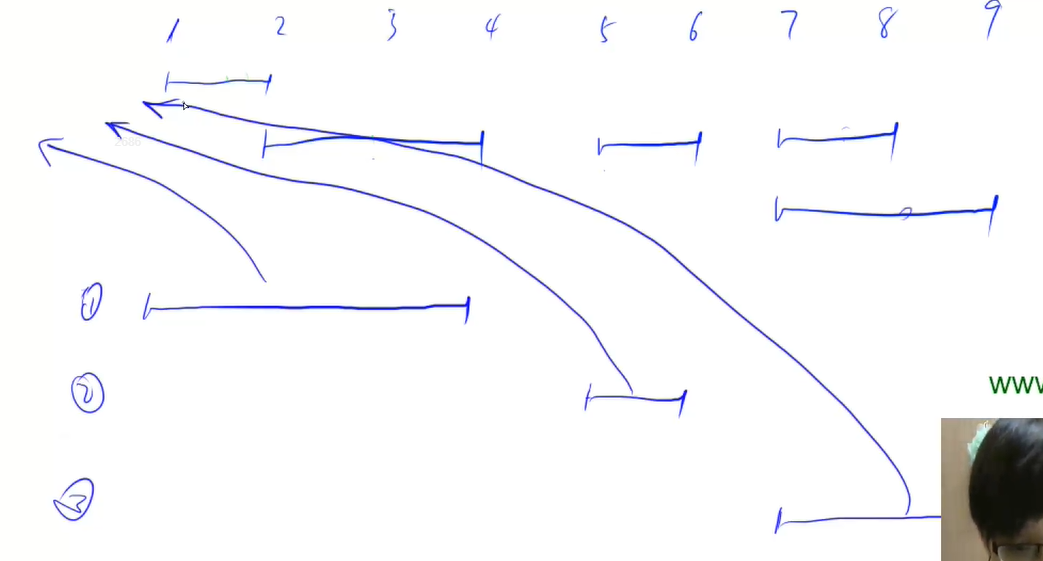
首先要对所有的区间进行左端点排序；

然后扫描整个区间，对可能的区间合并：大概分为3个情况，1：存在交集；2：包含关系；3：不存在任何交集。

整体思路：

1. 首先用pair存储输入的左端点和右端点，然后用sort对其进行排序，pair默认是按照左端点进行排序
2. 我们需要设置两个大的边界：默认为-2e9，，然后对排序后的每个pair进行操作，1.不存在交集的情况：判断当前维护的区间的最右边是否小于下一个区间的左端点，并且这个维护的区间不能是原来的初始区间，我们把这个区间加入到我们的答案，然后更新st 和 ed，第二种情况是存在交集，那么无论是当前区间的左端点还是下一个区间的左端点，我们根据排序都会选择默认的最左边的端点，后面我们只需要选择两个区间的最右边的右端点，那么我们就可以直接维护到合并后的区间，或者说是两个区间合并。
3. 最后我们需要把最后一个序列放到我们维护的区间里面！当然这个区间也不能是初试区间

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end()); //按左端点排序

    int st = -2e9, ed = -2e9; //ed代表区间结尾，st代表区间开头
    for(auto seg : segs)
    {
        if(ed < seg.first)  //情况1：两个区间不存在交集
        {
            if(ed != -2e9) res.push_back({st, ed}); //判断是否为初始区间
            st = seg.first, ed = seg.second; //维护区间2
        }
        //情况2：两个区间可以合并，且区间1不包含区间2，区间2不包含区间1
        else ed = max(ed, seg.second);

    }

    //剩下还有一个序列，但循环中没有放进res数组，因为它是序列中的最后一个序列 
    if(st != -2e9) res.push_back({st, ed});

    segs = res;
}


int main()
{
    int n;
    scanf("%d", &n);

    vector<PII> segs;

    for(int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }

    merge(segs);

    cout << segs.size() << endl;

    return 0;
}