这有啥不明白的，手把手画出来！

首先明确，为啥能用递归：
- 我们想计算 n 等级的坐标，知道 n-1 等级的坐标就行

然后思考怎么递归？

咱们首先规定，每个等级的坐标系原点是独特的，如下图。

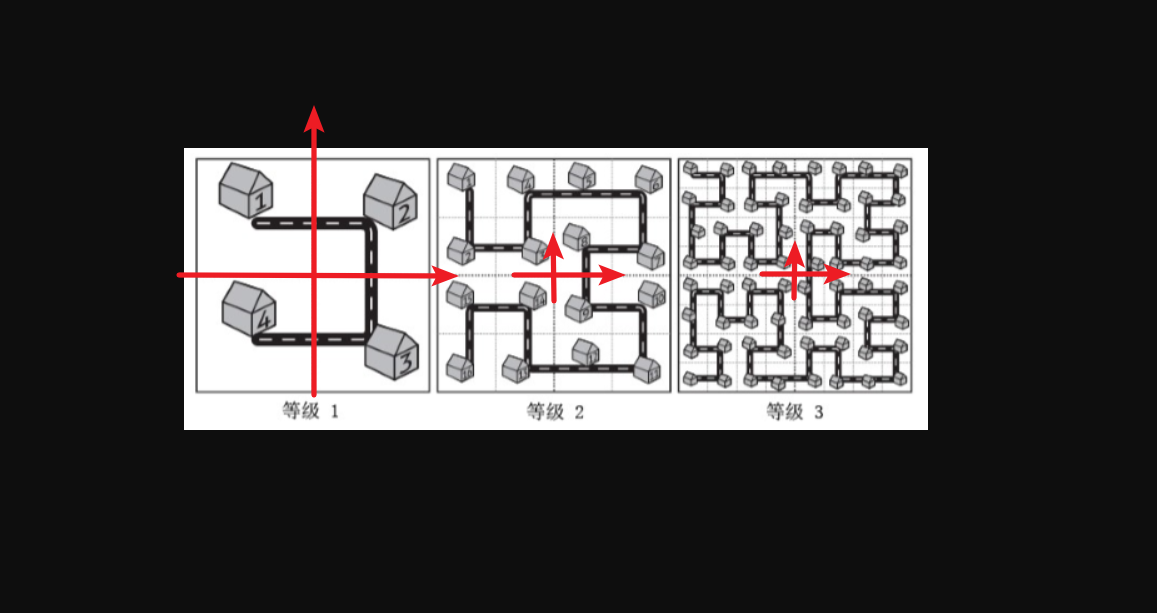
然后我们从特殊到一般，归纳推规律：
- 等级1这个块块，如果放到等级2里，有四种情况要讨论
- 等级1放到等级2的左上象限，则相当于顺时针旋转了 90° ，并且还要沿 y 轴翻转（为什么要沿 y 轴翻转呢？因为你注意每个编号的位置，不翻转，形状虽然对上了，但是编号顺序没对上）
- 等级1放到等级2的右上象限，则不用转
- 等级1放到等级2的右下象限，则不用转
- 等级1放到等级2的左下象限，则相当于逆时针旋转了 90° ，并且还要沿 y 轴翻转

转完了，因为我们现在从等级1到等级2了，因此坐标系原点也移动了，所以要在等级1的原有坐标基础上进行平移。

好了，我给你画个图，你就懂了。

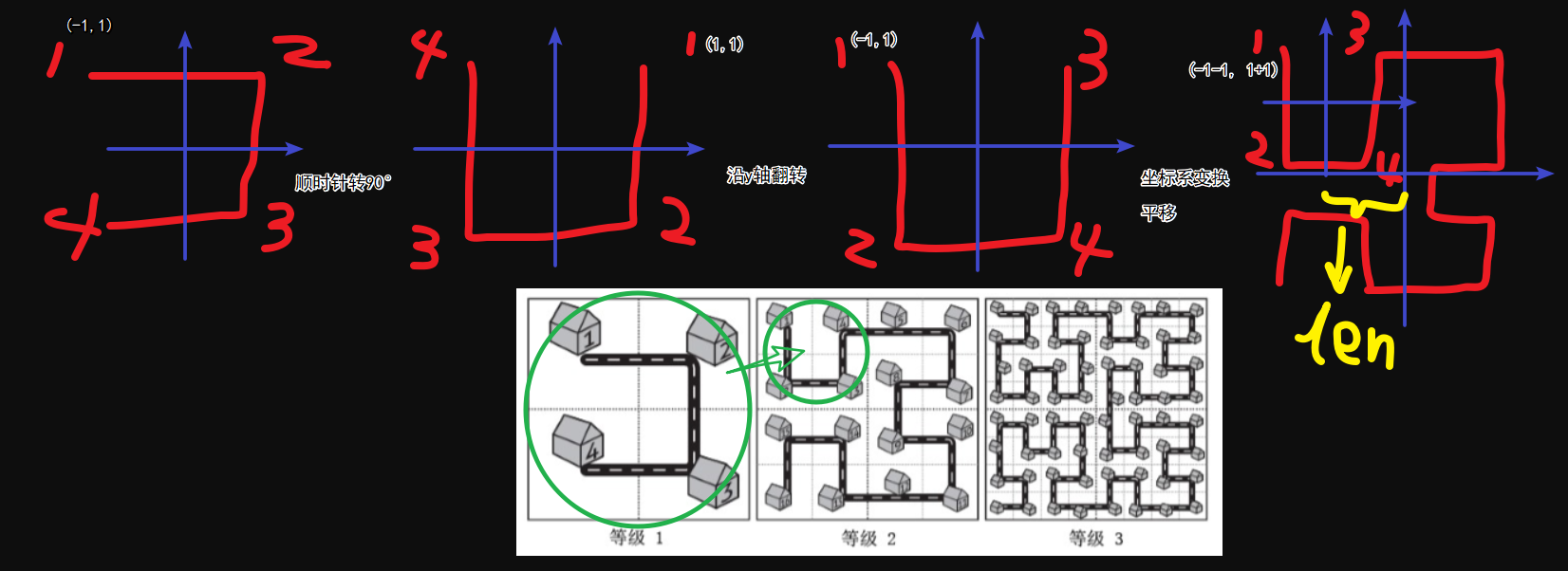
然后你再去看代码。

这里补充一点数学知识：
- 对于点 (x, y) ，沿原点顺时针旋转 90° ，将变为 (y, -x)
- 对于点 (x, y) ，沿原点逆时针旋转 90° ，将变为 (-y, x)
- 对于点 (x, y) ，以 y 轴为对称轴翻转将变为 (-x, y)

C++ 代码

#include <iostream>
#include <cstring>
#include <cmath>  // sqrt
#include <algorithm>

using namespace std;

typedef long long LL;
typedef pair<LL, LL> PLL;

PLL calc(LL n, LL m)
{
    /*
    * n: 等级
    * m: 坐标，从0开始计数
    */
    if (n == 0) return {0, 0};
    LL len = 1ll << (n - 1);  // 2^{n-1} 本等级内象限的边长/2
    LL cnt = 1ll << (2 * n - 2);  // 4^{n-1} 本等级内象限容量
    PLL pos = calc(n - 1, m % cnt);  // 上一等级的坐标信息
    LL x = pos.first, y = pos.second;
    int z = m / cnt;  // 处于哪个象限
    // 左上象限顺转90°（y,-x）沿y对称（-y,-x）更换原点（-y-len,-x+len）
    if (z == 0)
        return { - y - len, - x + len };
    // 右上象限更换原点（x+len,y+len）
    else if (z == 1)
        return { x + len, y + len };
    // 右下象限更换原点（x+len,y-len）
    else if (z == 2)
        return { x + len, y - len };
    // 左下象限逆转90°（-y,x）沿y对称（y,x）更换原点（y-len,x-len）
    return { y - len, x - len };
}

int main()
{
    int N;
    cin >> N;
    while (N --)
    {
        LL n, m1, m2;
        cin >> n >> m1 >> m2;
        PLL pos1 = calc(n, m1 - 1);
        PLL pos2 = calc(n, m2 - 1);

        double delta_x = (double) (pos1.first - pos2.first);
        double delta_y = (double) (pos1.second - pos2.second);
        // 等级1中 len 是单位长度，且表示象限的一半长即为 10 / 2 = 5
        printf("%.0lf\n", sqrt(delta_x * delta_x + delta_y * delta_y) * 5);
    }
}