最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

在 $n×n(1\le n \le 10)$ 的棋盘上放 $k(0\le k \le n^2)$ 个国王

国王可攻击相邻的 $8$ 个格子，求使它们 无法互相攻击 的 方案总数

八相邻：
通常意义上的八相邻指的是当前元素的上、下、左、右、左上、右上、左下、右下八个方向

分析

这种 棋盘放置类 问题，在没有事先知道一些特定 性质 的情况下来做，都会想到 爆搜

本题的数据规模，也是向着 爆搜 去设置的

如果我们直接 爆搜，则 时间复杂度 为 $O(2^{n^2})$ 是会超时的，因此会想到用 记忆化搜索 来进行优化

考虑一下如何进行 动态规划

由于在第 $i$ 层放置国王的行为，受到 $i-1$ 层和 $i+1$ 层以及 $i$ 层的状态影响

那么我们就可以规定从上往下枚举的顺序，这样考虑第 $i$ 层状态时，只需考虑 $i-1$ 层的状态即可

于是乎我们可以考虑把层数 $i$ 作为动态规划的 阶段 进行 线性DP

而第 $i$ 阶段需要记录的就是前 $i$ 层放置了的国王数量 $j$，以及在第 $i$ 层的 棋盘状态 $k$

这里先分析一下，哪些 棋盘状态 是合法的，哪些 棋盘状态的转移 是合法的

合法的棋盘状态

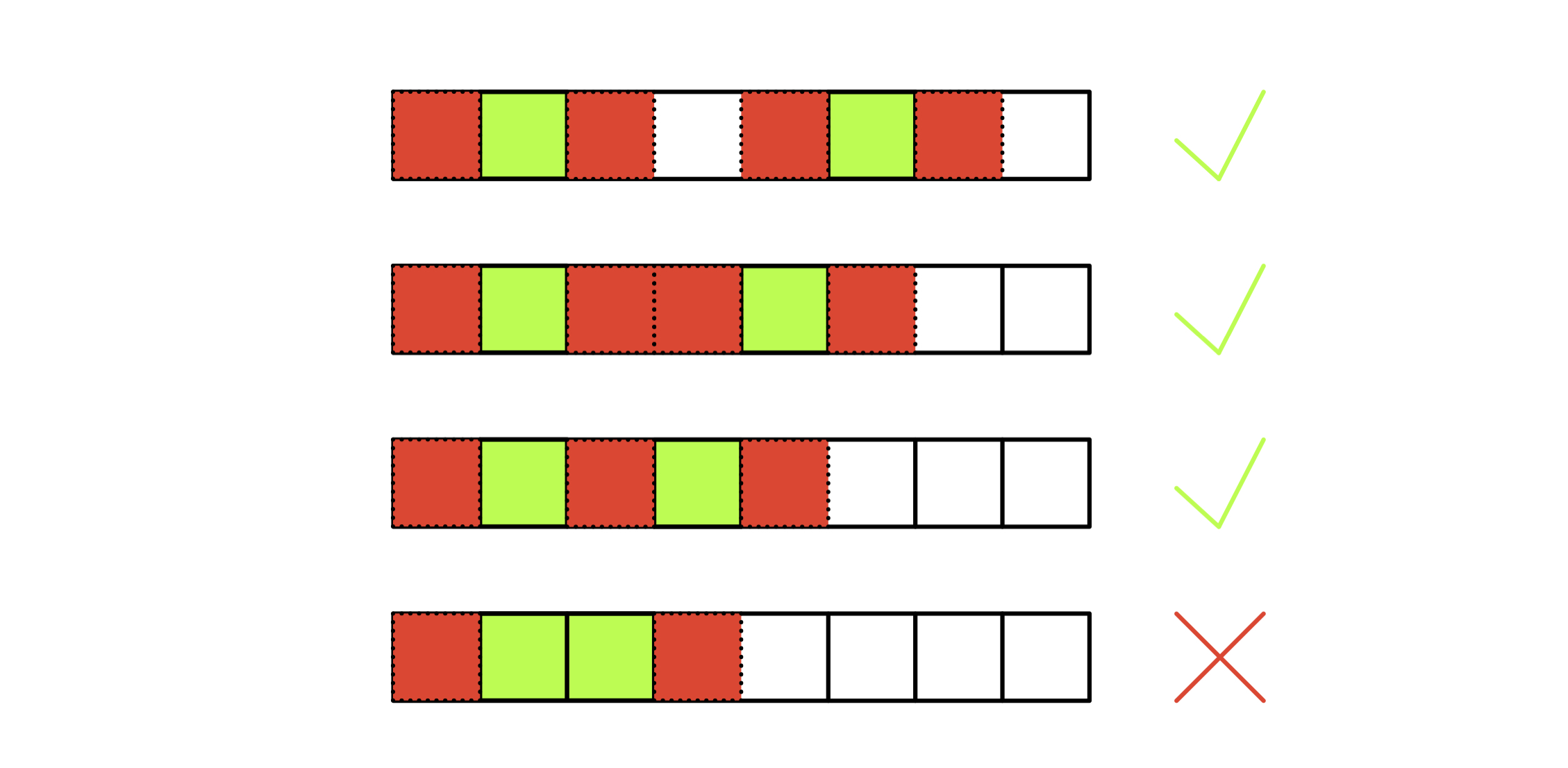
如上图所示，绿色方块为摆放国王的位置，红色方块为王的 攻击范围

只要任意王之间只要 不相邻，就是 合法的状态

合法的棋盘转移状态

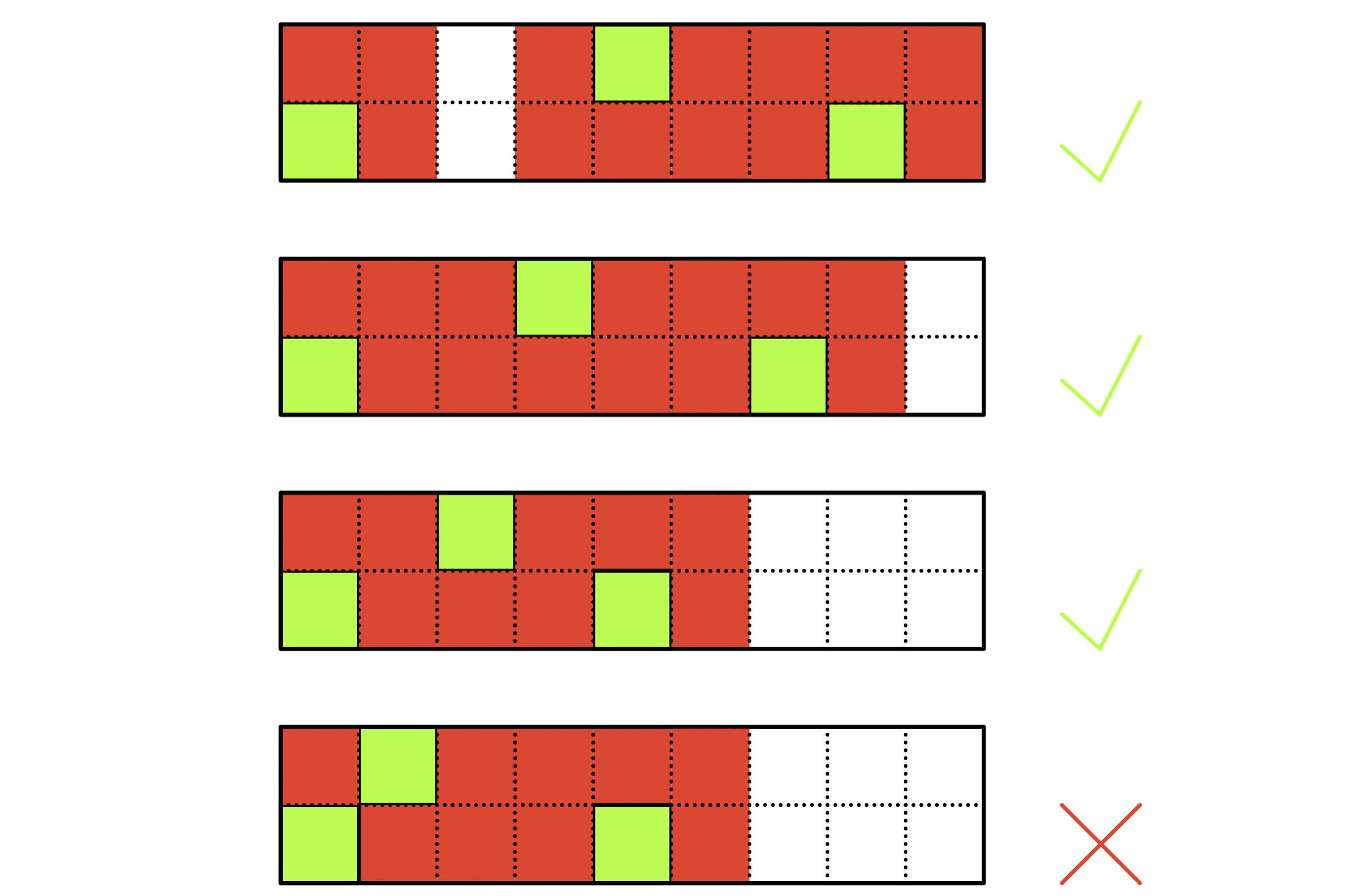
如上图所示，绿色方块为摆放国王的位置，红色方块为王的 攻击范围

只要任意王的 纵坐标不相邻，就是 合法的转移状态

我们可以用 二进制 来表示当前的状态

怎么用二进制表示状态？

若(state >> i) == 1 则表示在当前状态中，第 $k(0\le i\lt n)$ 个位置放置了国王（下标从 $0$ 开始）

再举一个简单的例子，见下图：

用二进制表示该状态，就是 $(00100010)_b$

于是，就有如下 闫氏DP分析

闫氏DP分析法

状态表示—集合$f_{i,j,k}:$ 考虑前 $i$ 层的棋盘，前 $i$ 层放置了 $j$ 个国王，且第 $i$ 层状态是 $k$ 的方案
状态表示—属性$f_{i,j,k}:$ 方案的总数 $Sum$
状态计算—$f_{i,j,k}:$
$$ f_{i,j,k} = \sum_{pre} f_{i-1,j-cnt_k,pre} $$
其中$pre$是枚举的能够与$k$合法存在于相邻行中的所有状态，$cnt_k$表示状态$k$中的国王数量

初始状态： $f_{0,0,0}$
目标状态： $f_{n,K,st} \quad(其中st为所有合法状态)$

这样直接做，时间复杂度是 $O(n^3 K 2^n 2^n)$ 是会超时的

但是我们可以通过预处理所有的 合法状态，以及合法的 相邻转移状态，以及 合法状态 摆放的国王数量

因为虽然状态很多，但是 合法状态 并不多， 合法的转移状态 更不多

Code

#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 11, M = 1 << N, C = N * N;

int n, m, K;
LL f[N][C][M];
int cnt[M];
vector<int> legal_state;
vector<int> state_trans[M];

bool check(int state)
{
    return !(state & state >> 1);
}
int count(int state)
{
    int res = 0;
    for (int i = 0; i < n; ++ i) res += state >> i & 1;
    return res;
}
int main()
{
    cin >> n >> K;
    //预处理所有合法状态
    for (int st = 0; st < 1 << n; ++ st)
        //检查当前状态是否合法
        if (check(st))
            legal_state.push_back(st),
            cnt[st] = count(st);
    m = legal_state.size();
    //预处理所有合法状态的合法转移
    for (auto cur_st: legal_state)
        for (auto to_st: legal_state)
            if (!(cur_st & to_st) && check(cur_st | to_st))//上下不相邻且纵坐标也不相邻
                state_trans[cur_st].push_back(to_st);
    //动态规划
    f[0][0][0] = 1;
    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j <= K; ++ j)
            for (auto &state: legal_state)
                for (auto &pre_st: state_trans[state])
                    if (j - cnt[state] >= 0)
                        f[i][j][state] += f[i - 1][j - cnt[state]][pre_st];
    //统计目标状态的所有方案数
    LL res = 0;
    for (auto state: legal_state) res += f[n][K][state];
    cout << res << endl;
    return 0;
}

滚动数组优化思路

由于第 $i$ 阶段状态只会用到第 $i-1$ 阶段的状态，因此我们可以采用滚动数组来优化空间

只贴上优化的部分

#include <iostream>
int main()  //不加这部分他高亮不出来，泪目T_T
{
    f[0][0][0] = 1;
    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j <= K; ++ j)
            for (auto &state: legal_state)
            {
                f[i & 1][j][state] = 0; //要先清空
                for (auto &pre_st: state_trans[state])
                    if (j - cnt[state] >= 0)
                        f[i & 1][j][state] += f[(i - 1) & 1][j - cnt[state]][pre_st];
            }
    LL res = 0;
    for (auto state: legal_state) res += f[n & 1][K][state];
    cout << res << endl;
}

y总的目标状态优化思路

我们可以很轻易的观察到，如果当前层的一个棋子都不摆，即$state = (000000)_b$

那么所有 合法的状态 都是该状态的 合法转移状态

翻译成白话就是：只要这层不摆东西，则上一层 只要合法，那一定可以转移到这一层的这个状态

因此我们可以把目标状态设为 $f_{n+1,K,0}$

该状态表示 考虑前 $n+1$ 层的棋盘，前 $n+1$ 层放置了 $K$ 个国王，且第 $n+1$ 层什么也没放的方案

根据我们之前提到的 状态转移 可知，该状态会把所有到第 $n$ 层的 合法状态 都转移到自己身上

这样最后我们就 不需要额外枚举所有的目标状态 了

完整代码如下：

#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N, C = N * N;

int n, m, K;
LL f[N][C][M];
int cnt[M];
vector<int> legal_state;
vector<int> state_trans[M];

bool check(int state)
{
    return !(state & state >> 1);
}
int count(int state)
{
    int res = 0;
    for (int i = 0; i < n; ++ i) res += state >> i & 1;
    return res;
}
int main()
{
    cin >> n >> K;
    //预处理所有合法状态
    for (int st = 0; st < 1 << n; ++ st)
        //检查当前状态是否合法
        if (check(st))
            legal_state.push_back(st),
            cnt[st] = count(st);
    m = legal_state.size();
    //预处理所有合法状态的合法转移
    for (auto cur_st: legal_state)
        for (auto to_st: legal_state)
            if (!(cur_st & to_st) && check(cur_st | to_st))//上下不相邻且纵坐标也不相邻
                state_trans[cur_st].push_back(to_st);
    //动态规划
    f[0][0][0] = 1;
    for (int i = 1; i <= n + 1; ++ i)
        for (int j = 0; j <= K; ++ j)
            for (auto &state: legal_state)
                for (auto &pre_st: state_trans[state])
                    if (j - cnt[state] >= 0)
                        f[i][j][state] += f[i - 1][j - cnt[state]][pre_st];
    //统计目标状态的所有方案数
    cout << f[n + 1][K][0] << endl;
    return 0;
}