最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

本题 有限字符集 为 $\{A,G,C,T\}$

题目给定 $n$ 个 模式串 $T_i (1 \le i \le n)$ 和 一个 主串 $S$

每次可以修改 主串 中的一个字符 $S[i]$

要求进行最少次 修改操作，使得 主串$S$ 中不存在 模式串 $T_i (1 \le i \le n)$ 的子串

求出该 操作次数 ，如果不行，输出 $-1$

分析

阅读本题解的前置知识： 自动机，AC自动机， 线性DP

基本思路和上一题 AcWing 1052. 设计密码【线性DP+KMP自动机模型】 一致
我就照搬一下上一题题解中的分析思路了

采用 线性扫描 的方法，进行 动态规划

考虑一个 单主串 与 多模式串 的 匹配算法，考虑使用 AC自动机 进行分析

考虑 阶段i 需要记录的状态也和上一题类似，是 自动机 的 状态j

自动机模型分析

依然举样例来分析，因为不同模式串构成的字典树不同，没法一概而论

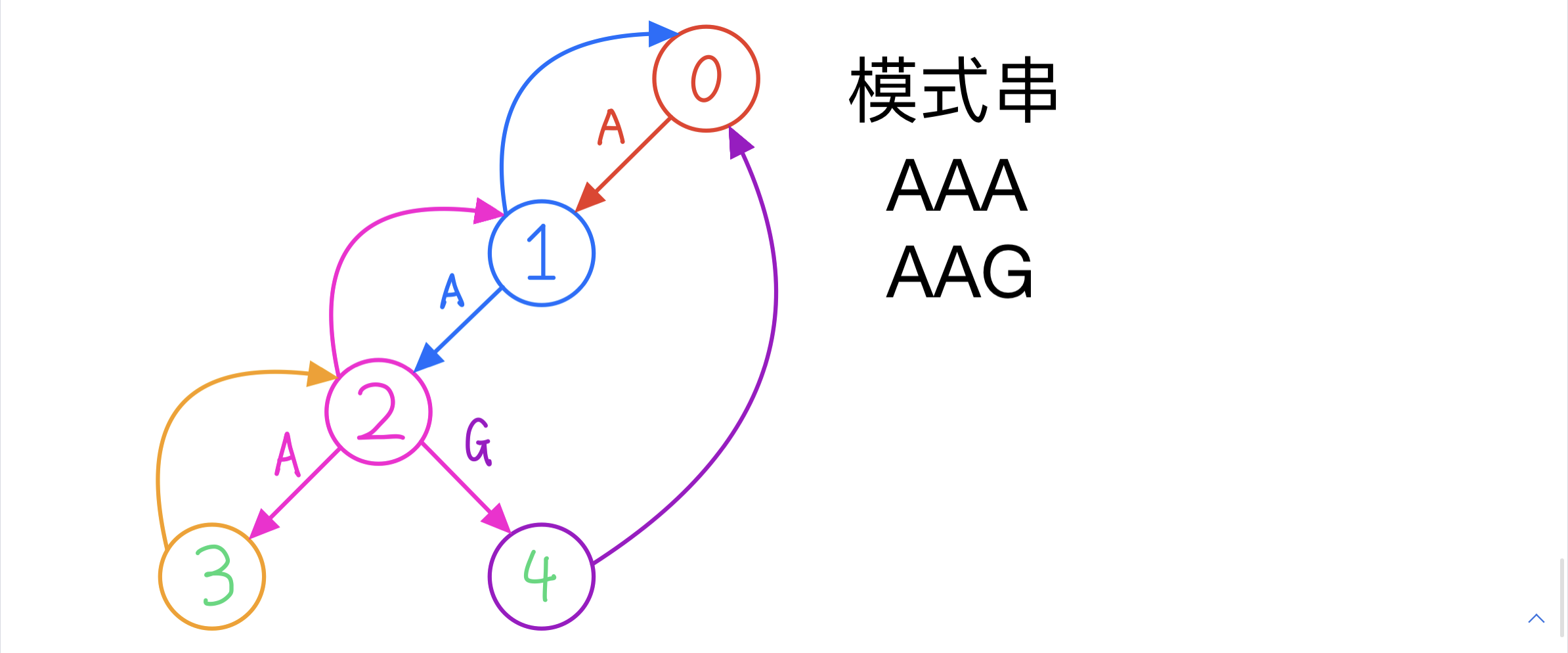
以 状态$j=2$为例

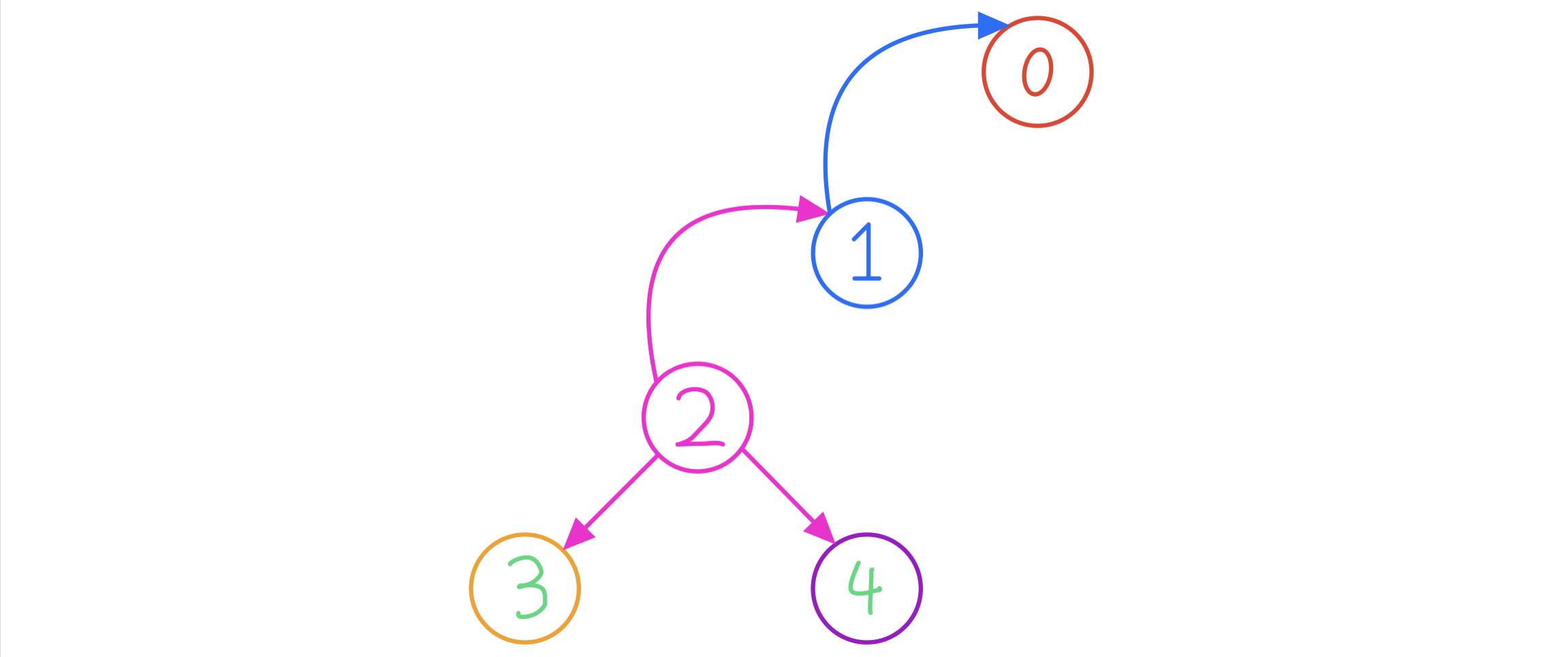
根据 AC自动机 的状态转移：

$$ trans_{j,c} = \begin{cases} j + 1, &if s_i=ch \\\ trans_{fail_j,ch} &else \end{cases} $$

对应于本样例就是：

1. ch是b，则最大长度增加一，对应到 $f_{i+1,j+1}$
2. ch不是b，则根据自动机跳到状态 $trans_{fail_j,ch}$，对应到 $f_{i+1,trans_{fail_j,ch}}$

闫氏DP分析法

状态表示—集合$f_{i,j}$: 考虑主串中前 $i$ 个字符，且当前自动机状态是 $j$ 的方案

状态表示—属性$f_{i,j}$: 方案的操作数最小 $Min$

状态计算$f_{i,j}$:

$$ f_{i+1, trans_{j,c}} = \min(f_{i, trans_{j,c}}, f_{i,j}) \quad(其中0\le c \le 3) $$

【注】：本题是求最小值，因此要把非初始状态初始化为正无穷

初始状态： $f_{0,0}$

目标状态： $f_{n,j} \quad j枚举的是所有自动机的状态$

Code 朴素写法

时间复杂度：$O(4Len_S \sum Len_{T_i})$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 55, M = 1010, K = 25;
const int INF = 0x3f3f3f3f;

int n;
char s[M];
int tr[N * K][4], cnt[N * K], idx;
int fail[N * K], q[N * K];
int f[M][N * K];

int get(char c)
{
    if (c == 'A') return 0;
    if (c == 'G') return 1;
    if (c == 'C') return 2;
    return 3;
}
void insert(char s[])
{
    int p = 0;
    for (int i = 0; s[i]; ++ i)
    {
        int u = get(s[i]);
        if (!tr[p][u]) tr[p][u] = ++ idx;
        p = tr[p][u];
    }
    cnt[p] = 1;
}
void build()
{
    int tt = -1, hh = 0;
    for (int i = 0; i < 4; ++ i)
        if (tr[0][i])
            q[ ++ tt] = tr[0][i];
    while (hh <= tt)
    {
        int u = q[hh ++ ];
        for (int i = 0; i < 4; ++ i)
        {
            if (tr[u][i])
                fail[tr[u][i]] = tr[fail[u]][i],
                q[ ++ tt] = tr[u][i];
            else
                tr[u][i] = tr[fail[u]][i];
        }
    }
}
void solve()
{
    //initializing
    memset(fail, 0, sizeof fail);
    memset(cnt, 0, sizeof cnt);
    memset(f, 0x3f, sizeof f);
    memset(tr, 0, sizeof tr);
    f[0][0] = 0;
    idx = 0;
    //input and build the AC Automaton
    for (int i = 1; i <= n; ++ i) cin >> s, insert(s);
    cin >> s + 1; build();
    int n = strlen(s + 1);
    //dp
    for (int i = 0; i < n; ++ i)
    {
        for (int j = 0; j <= idx; ++ j)
        {
            //枚举下一个字符
            for (int k = 0; k < 4; ++ k)
            {
                int cost = get(s[i + 1]) != k;  //修复下一个字符的费用
                //递归找到下一层的状态
                int p = tr[j][k];
                bool flag = true;
                int temp = p;
                while (temp)
                {
                    if (cnt[temp])
                    {
                        flag = false;
                        break;
                    }
                    temp = fail[temp];
                }
                //找到了，就更新
                if (flag) f[i + 1][p] = min(f[i + 1][p], f[i][j] + cost);
            }
        }
    }
    int res = INF;
    for (int j = 0; j <= idx; ++ j) res = min(res, f[n][j]);
    if (res == INF) res = -1;
    cout << res << endl;
}
int main()
{
    int T = 1;
    while (cin >> n, n)
    {
        cout << "Case " << T ++ << ": ";
        solve();
    }
    return 0;
}

Code（y总的优化思路）

OI爷的想法就是牛！

考虑一个长的匹配串，如果他的某一个前缀子串的最大相等前后缀（就是$fail[j]$） 出现了另一个模式串匹配成功的状态，则我们认为该状态就是 匹配成功状态

这样我们就不用每次枚举第 $i+1$ 个字符后，再额外进行 $fail$ 跳转枚举了

只需在建 AC自动机 时，构建 $fail$ 指针的跳转时，顺便记录 跳转到的状态 是否也会匹配上即可

由于 BFS 保证枚举状态 $j$ 时，所有 长度小于当前状态 的模式串以及 $fail$ 指针跳转都构建好了

因此，可以保证建立 $fail$ 指针时，他 跳转的状态 以及他 跳转的跳转的状态 是否是 匹配成功的状态 已经被更新出了

于是，通过该思路，就可以进行 y总的代码优化了

#include <iostream>
#include <cstring>

using namespace std;

const int N = 55, M = 1010, K = 25;
const int INF = 0x3f3f3f3f;

int n;
char s[M];
int tr[N * K][4], cnt[N * K], idx;
int fail[N * K], q[N * K];
int f[M][N * K];

int get(char c)
{
    if (c == 'A') return 0;
    if (c == 'G') return 1;
    if (c == 'C') return 2;
    return 3;
}
void insert(char s[])
{
    int p = 0;
    for (int i = 0; s[i]; ++ i)
    {
        int u = get(s[i]);
        if (!tr[p][u]) tr[p][u] = ++ idx;
        p = tr[p][u];
    }
    cnt[p] = 1;
}
void build()
{
    int tt = -1, hh = 0;
    for (int i = 0; i < 4; ++ i)
        if (tr[0][i])
            q[ ++ tt] = tr[0][i];
    while (hh <= tt)
    {
        int u = q[hh ++ ];
        for (int i = 0; i < 4; ++ i)
        {
            if (tr[u][i])
                fail[tr[u][i]] = tr[fail[u]][i],
                cnt[tr[u][i]] |= cnt[fail[tr[u][i]]],//看他跳转的状态是否是匹配成功状态
                q[ ++ tt] = tr[u][i];
            else
                tr[u][i] = tr[fail[u]][i];
        }
    }
}
void solve()
{
    //initializing
    memset(fail, 0, sizeof fail);
    memset(cnt, 0, sizeof cnt);
    memset(f, 0x3f, sizeof f);
    memset(tr, 0, sizeof tr);
    f[0][0] = 0;
    idx = 0;
    //input and build the AC Automaton
    for (int i = 1; i <= n; ++ i) cin >> s, insert(s);
    cin >> s + 1; build();
    int n = strlen(s + 1);
    //dp
    for (int i = 0; i < n; ++ i)
    {
        for (int j = 0; j <= idx; ++ j)
        {
            //枚举下一个字符
            for (int k = 0; k < 4; ++ k)
            {
                int cost = get(s[i + 1]) != k;  //修复下一个字符的费用
                int p = tr[j][k];               //下一个字符的自动机状态
                if (!cnt[p]) f[i + 1][p] = min(f[i + 1][p], f[i][j] + cost);
            }
        }
    }
    int res = INF;
    for (int j = 0; j <= idx; ++ j) res = min(res, f[n][j]);
    if (res == INF) res = -1;
    cout << res << endl;
}
int main()
{
    int T = 1;
    while (cin >> n, n)
    {
        cout << "Case " << T ++ << ": ";
        solve();
    }
    return 0;
}