最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个字符串 $T$，和一个整数 $N$

现需设计一个密码 $S$, $S$ 需满足：

1. $S$ 的长度是 $N$
2. $S$ 只包含小写英文字母
3. $S$ 不包含子串 $T$

求该密码的 方案数，答案对 $10^9+7$ 取模

分析

首先读者需要了解一部分自动机的概念，我推荐一下OI-Wiki的这篇博客 自动机 - OI Wiki

了解自动机是学字符串的基础，之后学习 AC自动机、 KMP 、 后缀自动机SAM 都有很大的帮助

求方案数 的题目难免不会让人想到用 动态规划 来求解

设计一个 合法的密码，从前往后 线性构造 是一个不错的枚举方案

因为如果 当前设计的密码 是合法的话，在他后面添上一个 新字符，可能会导致 新密码不合法 的情况，只有可能是 新密码 的 后缀子串 中出现了 $T$

通过 线性构造 的方法，我们只需判断 后缀子串 中是否出现 $T$ 即可

那么如果我们想用线性DP来求解，应该如何记录当前的状态呢？

首先，毫无疑问是用当前构造的密码长度 $i$ 作为 线性DP 的阶段

可是如何记录当前的长度为 $i$ 的字符串的 后缀 与 字符串 $T$ 的匹配情况呢？

关于 单母串 和 单模式串 的 在线匹配，会自然而然的想到一个 字符串算法 —— 前缀函数与KMP

借用 KMP 的思想，我们可以用参数 $j$ 来表示当前 母串后缀 与 模式串 匹配的 最大长度

KMP 求前缀函数的 在线性 ，使得我们可以任意枚举第 $i+1$ 个字符后，快速获得其 前缀函数值

该 前缀函数值 也就是 $i+1$ 状态对应的新的 $j$ 的值 $\delta(\pi(i),ch)$

于是我们就可以利用 $f_{i,j}$ 来更新 $f_{i+1,\delta(\pi(i),ch)}$ 的状态，具体看下面的分析：

自动机模型分析

本题对于不同的 模式串，自动机模型 不同，因此我以 模式串 ababc 举例

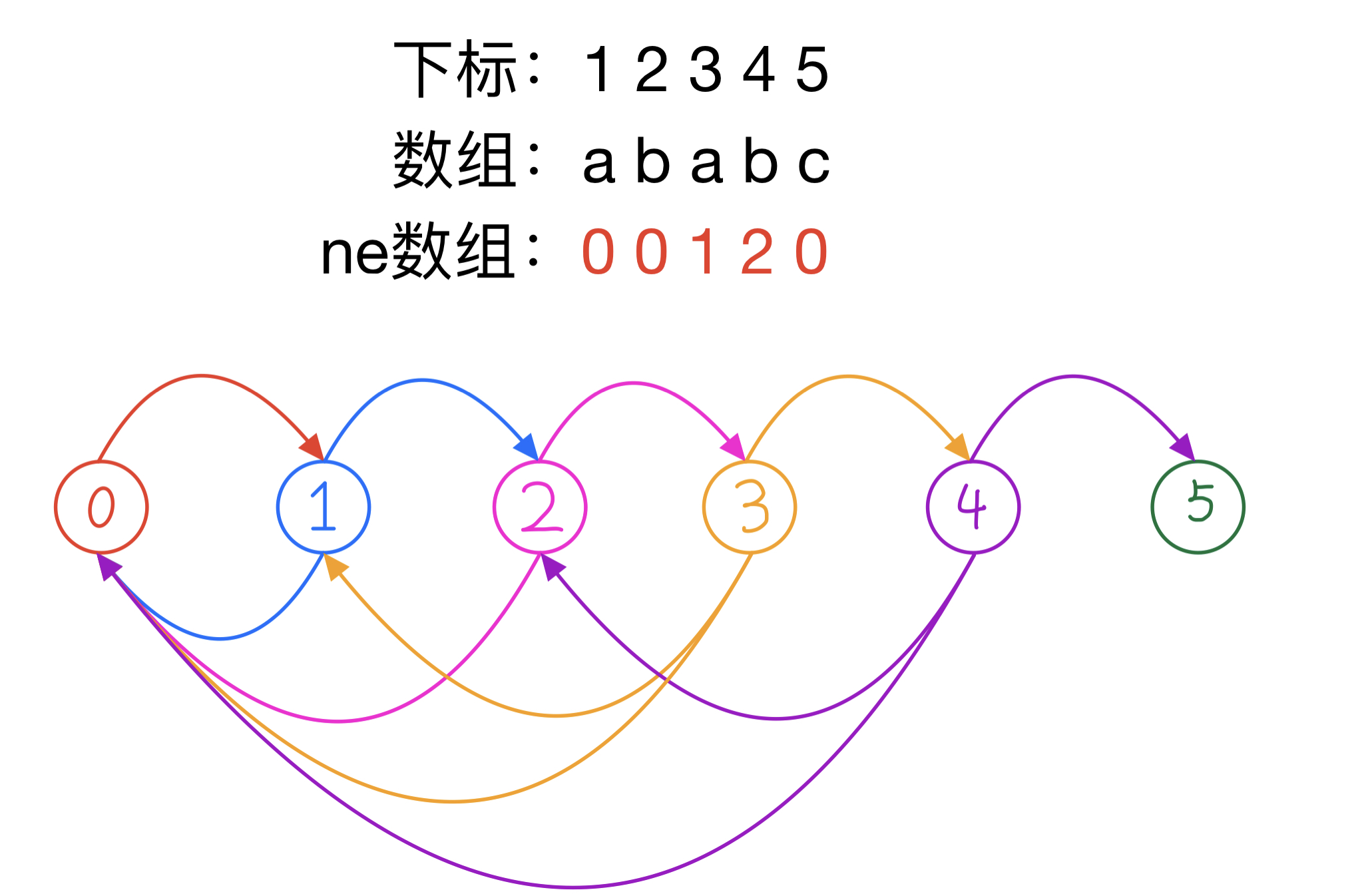
先看上面的转移

该转移表示 $s_{i+1} = ch$ 而发生的转移，也就是枚举的字符 $ch$ 刚好等于 模式串 的第 $i$ 个字符

于是就会使 最大长度 增加 $1$，即 $f_{i+1,j+1} ~+=~ f_{i,j}$

然后我再具体分析一下这个状态机里的 $f_{i,3}$ 状态（其他状态可以类比）

我们枚举下一个添加的字符（即枚举 $s_{i+1}$ 的字符 $ch$）时：

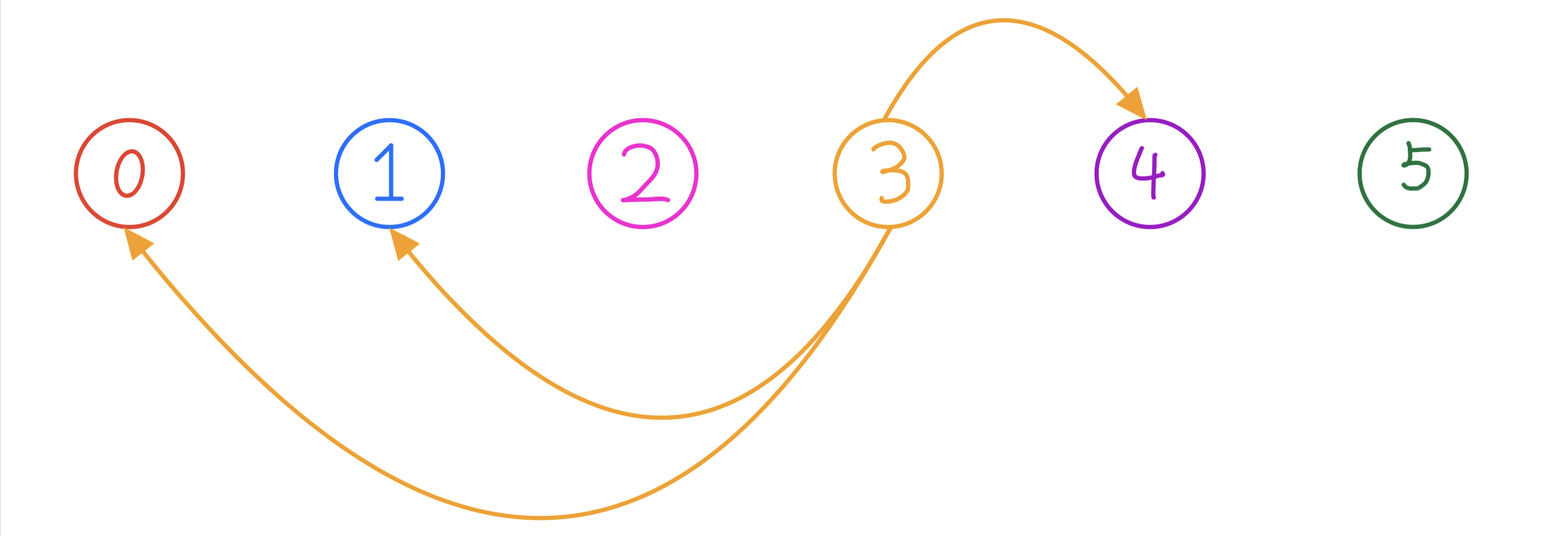
根据如下转移函数：

$$ \delta(i,ch) = \begin{cases} i+1 &s_{i+1}=ch \\\ \delta(\pi(i),ch) &s_{i+1}\ne ch \text{^} i > 0 \\\ 0 &s_{i+1}\ne ch \text{^} i = 0\\\ \end{cases} $$

对应于本样例就是：

1. $ch$ 是 $b$，则最大长度增加一，对应到 $f_{i+1,j+1}$
2. $ch$ 不是 $b$，则根据自动机跳到位置 $p$，如果 $s_{p+1} = ch$ 则最大长度增加一，对应到 $f_{i+1,p+1}$
3. $ch$ 不是 $b$，则根据自动机跳到位置 $0$，如果 $s_{1} \ne ch$ 则最大长度为0，对应到 $f_{i+1,0}$

闫氏DP分析法

状态表示—集合$f_{i,j}$： 考虑构造一个 长度 为 $i$ 的密码，且后缀与模式串匹配的 最大长度 为 $j$ 的方案

状态表示—属性$f_{i,j}$： 方案的总数 $Sum$

状态计算$f_{i,j}$：

$$ f_{i+1,\delta(\pi(j),ch)} ~+=~ f_{i,j} \quad(其中 a\le ch\le z) $$

Code

时间复杂度： $O(26N^3)$

初始状态： $f_{0,0}$

目标状态： $f_{n,j} \quad 其中j\in[0,M)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 55, mod = 1e9 + 7;

int n, m;
char s[N];
int f[N][N], ne[N];

int main()
{
    cin >> n >> s + 1;
    m = strlen(s + 1);
    //KMP预处理前缀表
    for (int i = 2, j = 0; i <= m; ++ i)
    {
        while (j && s[i] != s[j + 1]) j = ne[j];
        if (s[i] == s[j + 1]) ++ j;
        ne[i] = j;
    }
    //DP
    f[0][0] = 1;
    for (int i = 0; i < n; ++ i)
    {
        for (int j = 0; j < m; ++ j)
        {
            for (char ch = 'a'; ch <= 'z'; ++ ch)   //枚举第i+1个字符
            {
                int ptr = j;    //计算枚举到第i+1个字符后，后缀匹配的最大长度
                while (ptr && s[ptr + 1] != ch) ptr = ne[ptr];
                if (s[ptr + 1] == ch) ++ ptr;
                f[i + 1][ptr] = (f[i + 1][ptr] + f[i][j]) % mod;    //更新i+1的状态
            }
        }
    }
    //统计所有目标状态
    int res = 0;
    for (int j = 0; j < m; ++ j) res = (res + f[n][j]) % mod;
    cout << res << endl;
    return 0;
}