最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个长度为 $N$ 的数组 $w$，数组的第 $i$ 个元素 $w_i$ 表示第 $i$ 天的股票 价格

1. 一次买入一次卖出为一笔 合法交易，且不能同时产生多笔交易（必须在再次购买前出售掉之前的股票）

2. 卖出股票后，无法在第二天买入股票（冷冻期为1天）

设计一个方案，使得总利润最大

分析

本题是 股票买卖系列 的 第五版，我们可以沿用 第四版 继续做一些改变

与 第四版 相关的 dp分析 和 状态机模型分析 ，在这里我不会具体展开

想了解 第四版 的，具体可以参考 股票买卖 IV【线性DP+状态机模型DP+滚动数组优化】

在这篇博客里，我有详细的分析

以 线性 的方式 动态规划，考虑第 i 阶段/天 的状态，需要记录的参数有哪些：

1. 第 i 天的 决策状态：
   1. (j=0) 当前没有股票，且不处于冷冻期 （空仓）
   2. (j=1) 当前有股票 （持仓）
   3. (j=2) 当前没有股票，且处于冷冻期 （冷冻期）

注意：这里的 冷冻期 状态，实际意义是指当天卖出了股票，所以 后一天是没法交易

状态机模型分析

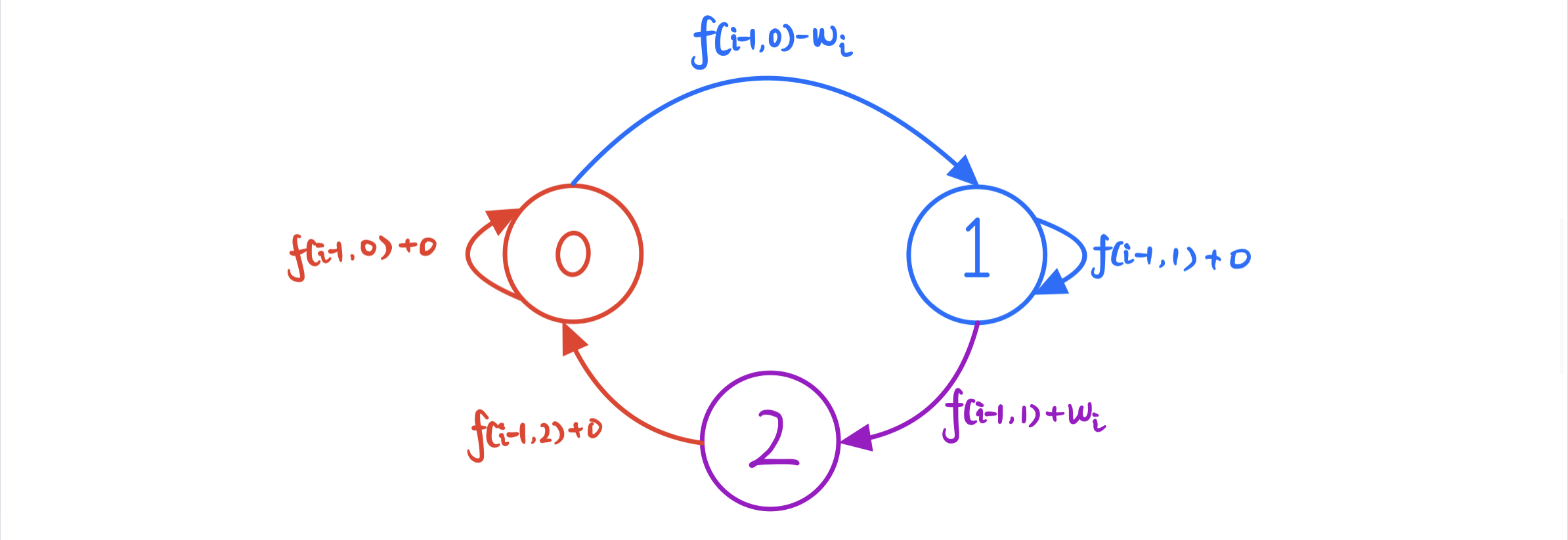
1. 如果第 i 天是 空仓 (j=0) 状态，则 i-1 天可能是 空仓 (j=0) 或 冷冻期 (j=2) 的状态
2. 如果第 i 天是 冷冻期 (j=2) 状态，则 i-1 天只可能是 持仓 (j=1) 状态，在第 i 天选择了 卖出
3. 如果第 i 天是 持仓 (j=1) 状态，则 i-1 天可能是 持仓 (j=1) 状态 或 空仓 (j=0) 的状态 （买入）

闫氏DP分析法

状态表示$f_{i,j}$—属性: 考虑前 i 天股市，当前第 i 天的状态是 j 的方案

状态表示$f_{i,j}$—集合: 方案的总利润 最大Max

状态计算$f_{i,j}$:

$$ \begin{cases} \quad f_{i,0} = \max\Big( f_{i-1,0}, f_{i-1, 2} \Big) \\\ \quad f_{i,1} = \max\Big( f_{i-1,1}, f_{i-1, 0} - w_i \Big) \\\ \quad f_{i,2} = f_{i-1,1} + w_i \\\ \end{cases} $$

初始状态： $f_{0,0}$
目标状态： $f_{n,j} \quad 其中j = 0,2$

Code

时间复杂度： $O(N)$

空间复杂度： $O(N)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n;
int w[N];
int f[N][3];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for (int i = 1; i <= n; ++ i)
    {
        f[i][0] = max(f[i - 1][0], f[i - 1][2]);
        f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
        f[i][2] = f[i - 1][1] + w[i];
    }
    cout << max(f[n][0], f[n][2]) << endl;
    return 0;
}

滚动数组优化

时间复杂度： $O(N)$

空间复杂度： $O(1)$

思路同 01背包

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n;
int w[N];
int f[2][3];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for (int i = 1; i <= n; ++ i)
    {
        f[i & 1][0] = max(f[(i - 1) & 1][0], f[(i - 1) & 1][2]);
        f[i & 1][1] = max(f[(i - 1) & 1][1], f[(i - 1) & 1][0] - w[i]);
        f[i & 1][2] = f[(i - 1) & 1][1] + w[i];
    }
    cout << max(f[n & 1][0], f[n & 1][2]) << endl;
    return 0;
}