最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划
题目描述
给定一个长度为 $N$ 的数组 $w$，数组的第 $i$ 个元素 $w_i$ 表示第 $i$ 天的股票 价格
一次买入一次卖出为一笔 合法交易，且不能同时产生多笔交易（必须在再次购买前出售掉之前的股票）
设计一个方案，使得总 合法交易数 不超过 $k$ 次，总利润最大
接 股票买卖II 的拓展思考
如果你做过前几版的 股票买卖 可以只看下面这几行的分析
AcWing 1055. 股票买卖 II DP + 贪心 双解 中分析过 第二版 的解法
而本题是 股票买卖 系列的 第四版
在 第二版 上， 额外 限制了 总交易的次数，因此 第二版 中的 贪心思路 不再适用
我们可以在 第二版 的 DP模型 上，额外加上记录 当前交易笔数 的参数即可
原题分析
对于第 $i$ 天 购入 的股票，当且经当第 $j(i \le j)$ 天才能 卖掉，获得的 利润 为 $w_j-w_i$
由此可知求解 股票交易 问题是一个 线性 的过程，于是我们思考一下能否用 线性DP 进行 状态记录 和 转移
线性DP如何记录当前的状态？
我们以当前递推到的天数，作为 线性DP 的阶段
对于递推到的第 $i$ 天来说，我们需要记录的信息有：
- 在完成第 $i$ 天的决策后，状态是持仓($k=1$)还是空仓($k=0$)
- 在第 $i$ 天交易完成时，总共完成的 完整 的交易数 $j$ (题目规定一次买入一次卖出是一笔 完整的交易)
那么如何利用该状态表示出题设中的状态转移行为呢？
- 买入行为：k=0 $\rightarrow$ k=1
- 卖出行为：k=1 $\rightarrow$ k=0
- 持仓行为：k=1 $\rightarrow$ k=1
- 空仓行为：k=0 $\rightarrow$ k=0
于是，有了如下的 闫氏DP分析法
闫氏DP分析法
状态表示$f_{i,j,k}$—集合： 考虑前 i 天的股票，第 i 天的 决策 是 k，且完成的 完整交易数 为 j 的方案
状态表示$f_{i,j,k}$—属性： 方案的总利润 最大MAX
状态计算$f_{i,j,k}$：
$$ \begin{cases} f_{i,j,0} = \max\Big( f_{i-1, j, 0}, f_{i-1, j - 1, 1} + w_i \Big) \\\ f_{i,j,1} = \max\Big( f_{i-1, j, 1}, f_{i-1, j, 0} - w_i \Big) \end{cases} $$
接下来用 状态机模型 解释一下状态计算
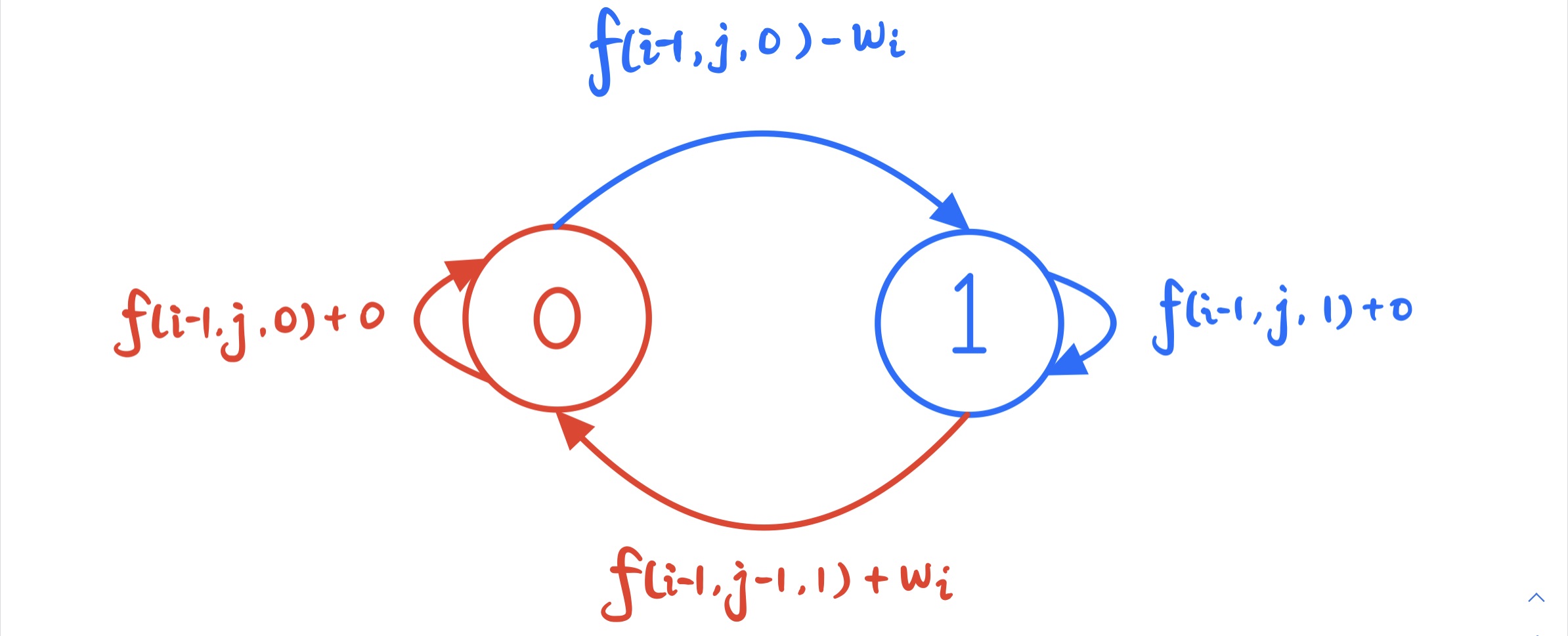
状态机模型DP
- 第 i 天状态是持仓状态(j=1)，则第 i 天可能产生的行为是 买入行为 或 持仓行为
- 第 i 天状态是空仓状态(j=0)，则第 i 天可能产生的行为是 卖出行为 或 空仓行为
【注】：卖出行为 会构成一次完整的交易，所以进行该类转移时， j 的参数也要变动
Code
时间复杂度： $O(N \times K)$
空间复杂度： $O(N \times K)$
初始状态: $f(0,0,0)$
目标状态: $f(n,j,0)\quad 其中 0\le j \le k$
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 110;
int n, k;
int w[N];
int f[N][M][2];
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; ++ i) cin >> w[i];
memset(f, -0x3f, sizeof f);
f[0][0][0] = 0; //初始状态f[0][0][0]
for (int i = 1; i <= n; ++ i)
{
for (int j = 0; j <= k; ++ j)
{
f[i][j][0] = f[i - 1][j][0];
if (j) f[i][j][0] = max(f[i][j][0], f[i - 1][j - 1][1] + w[i]);
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
}
}
int res = 0;
for (int j = 0; j <= k; ++ j) res = max(res, f[n][j][0]); //目标状态f[n][j][0]
cout << res << endl;
return 0;
}
滚动数组优化
很多 线性DP 都可以用此类优化，详见 【01背包DP模型+朴素优化】
时间复杂度： $O(N \times K)$
空间复杂度： $O(K)$
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 110;
int n, k;
int w[N];
int f[2][M][2];
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; ++ i) cin >> w[i];
memset(f, -0x3f, sizeof f);
f[0][0][0] = 0; //初始状态f[0][0][0]
for (int i = 1; i <= n; ++ i)
{
for (int j = 0; j <= k; ++ j)
{
f[i & 1][j][0] = f[(i - 1) & 1][j][0];
if (j) f[i & 1][j][0] = max(f[i & 1][j][0], f[(i - 1) & 1][j - 1][1] + w[i]);
f[i & 1][j][1] = max(f[(i - 1) & 1][j][1], f[(i - 1) & 1][j][0] - w[i]);
}
}
int res = 0;
for (int j = 0; j <= k; ++ j) res = max(res, f[n & 1][j][0]); //目标状态f[n][j][0]
cout << res << endl;
return 0;
}
题目没说太清楚，一次只能买入一张股票。
我就是有点不太理解j之间的关系，感觉y总那里一下讲得有点只能意会不能言传的感觉
看题目,题目说买入卖出后才算一次交易，也就是说在i想要买入,必须在i之前完成一次交易即卖出货物
只有买入的时候才算新的交易开始，j-1变为j;
卖出的时候是这轮交易完成，所以j不变
这个问题的关键在于题目上给出的定义，一次买入一次卖出为一笔合法交易。
y总是将买入看作进行了一次交易，轮次的增加是在进行买入时进行更新，后面的卖出是在完成一个完整的交易。
所以f[i ,j , 0] 从f[ i-1, j, 1]转移过来，是在完成在第i-1天买入的完整交易，轮次是同一轮，所以j不变。
同理：f[i , j , 1] 从f[i , j-1, 0] 转移过来，是在第i天开启新的一轮交易，增加一轮的轮次 j-1 变为 j。
f[i, j ,1] 表示第i天买入，与f[i+1, j, 0]就是第i+1天卖出（如果i+1天卖出的话）是同轮次。
优化空间的时候，不需要&1，只要改变一下for循环里面的枚举顺序就不会发生串联了
但是 只用到i-1层的话，巨巨的&1就可以看作是一种通法了，比如这题的下一题就可以用这种通法优化空间有效防止串联
我的理解不知道对不对，这里的 i & 1 相当于 % 2，因为这个问题中迭代 “i” 只需要“i - 1”的状态，如果某个问题中”i“ 需要 “i - 1” 和 “i - 2”的状态的话。滚动数组优化只需要 % 3就可以了。
如果依赖前两个，”& 3” 会更好
为什么你这里j为什么从0可以开始 y总的从1开始
因为它的状态表示是已经完成了j次交易，而y总是正在进行第j次交易，状态定义不同，第一种刚开始还没有交易，完成了0次，j从0开始，第二种是在进行第1次交易，j从1开始
空间优化版本,还想了一下hh.居然可以&1操作,开[2]就可以,6的
有一点就是 memset(f, -0x3f, sizeof f);这个全部负无穷的意义是啥，为什么不能全部初始化成0
f[i,0,1]含义：在前i 天，经过了0次交易，持有股票。股票从天下掉下来的吗？很显然这是不合法的状态，为了避免合法状态错误的引用了不合法状态，需要把所有不合法的状态设置为-inf。哪些是不合法的状态呢？当然是所有f[i][0][1],那合法状态呢？f[i][0][0]
经过了0次交易，并持有股票有什么问题吗？？？麻烦好好审题
初始化0的话，f[0][j][1]是0，第一次买股票时f[i][j][0]-w[i] 是小于0的，小于f[ 0][j][1]，就永远不会买股票
原来如此，大佬nb！
我想问下，三维版本这里不可以优化成二维吗，我这样写是哪里出了问题吗
请问什么画的图，大佬？tql
应该是平板。题解是可以自己弄图上去的
确实好像
大佬，你第二版空间复杂度假了，w数组的复杂度也是O(N)的，可以一遍读入一边输出来把w优化掉
大佬大佬！！！ 为啥这里要特判一下雅 if (j) f[i & 1][j][0] = max(f[i & 1][j][0], f[(i - 1) & 1][j - 1][1] + w[i]);
j = 0时，j -1 越界
嗯嗯 谢谢
Orz
巨巨, 为什么f[i][j][0/1]不定义成 前i天 完成不超过j次交易 且 决策为0/1的集合?
可以，不过初始化会有点麻烦，改成不超过的初始化如下：
巨巨 厉害了 !!! 但是为什么要这样初始化?
对于集合范围的定义，除了状态转移，还要注意状态的起点
去找符合集合定义的起点，再把不符合的全部初始化掉就好了
是不是可以理解为 只初始化为合法的起点, 然后把剩下的全初始化为 相应的非法状态?
可以这么理解
本题假设是按照 f[i][j][0/1]定义成 前i天 完成不超过j次交易 且 决策为0/1的集合, 那么此时的起点为f[0][j][0/1],按照集合定义可以发现都是f[0][j][0]都是合法起点.剩余的均为-INF
若按照 前i天 已经完成j次交易 且 决策为0/1的集合,那么此时起点为f[0][j][0/1] 可以发现只有f[0][0][0]为合法起点.剩余均为-INF .
巨巨 orz
只需要初始化第 0 维就可以了, 没必要初始化 i = 1 to n 维
woc大佬我看懂了，谢谢大佬，orzorz
` if (j) f[i][j][0] = max(f[i][j][0], f[i - 1][j - 1][1] + w[i]);这个如果是由
f[i - 1][j - 1][1]转移的话，怎么可以卖了第i天的股票呀啊这，为什么不可以卖了第
i天的股票呀我傻了 我的问题😭
同一张股票的不同价格！ 😭
hh
好的谢谢qwq
都仰慕您好久了！
我没有OI经历，不太了解hh。
我大学学的算法，而且是数学系的，不是科班，你可以问问 mrk、wh、抽风他们
原来彩铅佬是数学系的，感觉证明写得很严谨!!!
或者需要重点学什么？
大佬太牛了！！我最近要考NOI 提高组，大佬可以推荐一些学习资料或者做的题吗？
彩铅佬！！！
😂你好