最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

街道上有 $N$ 家店铺，按照顺序从 $1$ 到 $N$ 排好

第 $i$ 家店铺的财产是 $w_i$

大盗阿福如果偷了第 $i$ 家店铺，则他不能偷 相邻的店铺，否则会被抓起来

帮助大盗阿福找出一种偷盗 方案，使得获得的 总财产最大

分析

这是一道经典的 线性DP 问题

为何本题可以线性DP求解？

先考虑的问题是，我们能否按照从 $1$ 到 $N$ 的 线性顺序 找出 最优解

答案当然是可以的，因为每家店铺在第 i 次被偷和在第 j 次被偷，获得的 价值 是一样的

对于一个 非线形 顺序的最优解，可以通过有限次交换，在保证答案不会减少的情况下，变成 线性顺序

于是我们从前往后 线性DP 即可

考虑如何表示当前的状态？

需要记录的有，当前线性递推到第 i 家店铺，以及对于第 i 家店铺，我们选择 偷 或者 不偷

于是就有了如下的 闫氏DP分析法

闫氏DP分析法

状态表示$f_{i,j}$—属性: 考虑前 i 家店铺，当前第 i 家店铺选择 偷(j=1) 或者 不偷(j=0) 的方案

状态表示$f_{i,j}$—集合: 方案的总价值 最大Max

状态计算$f_{i,j}$:

$$\begin{cases} f_{i,0} = \max\Big( f_{i-1,1}, f_{i-1, 0} \Big) \\\ f_{i,1} = f_{i-1,0} + w_i \end{cases}$$

接下来解释一下这里的状态计算

状态机模型分析

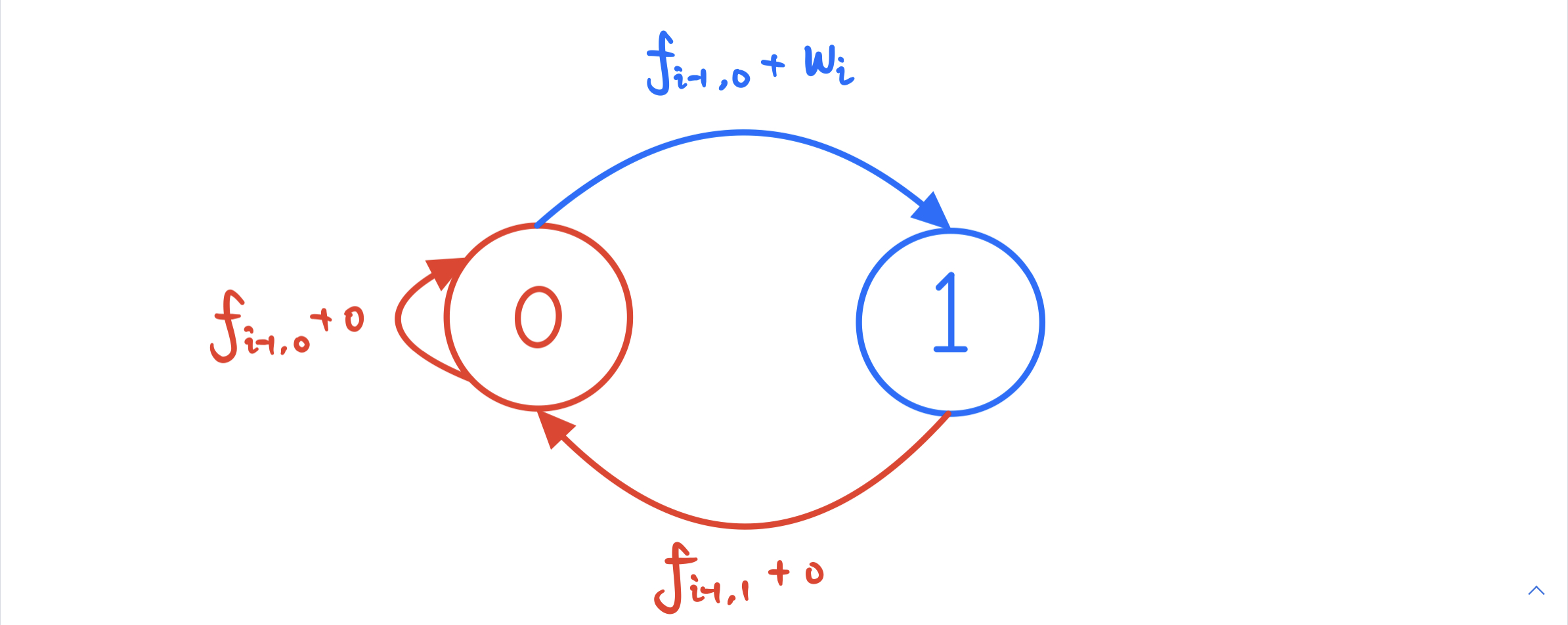
如果要偷第 i 家店铺，则第 i-1 店铺不能被偷：$f_{i,1} = f_{i-1,0} + w_i$

如果不偷第 i 家店铺，则第 i-1 店铺任意安排：$f_{i,0} = \max\Big( f_{i-1,1}, f_{i-1, 0} \Big)$

Code

时间复杂度: $O(N)$

空间复杂度: $O(N)$

初始状态： f[0][0]

目标状态： f[n][0] 和 f[n][1]

#include <iostream>

using namespace std;

const int N = 1e5 + 10, INF = 0x3f3f3f3f;

int n;
int w[N];
int f[N][2];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];
    for (int i = 1; i <= n; ++ i)
    {
        f[i][0] = max(f[i - 1][1], f[i - 1][0]);
        f[i][1] = f[i - 1][0] + w[i];
    }
    cout << max(f[n][0], f[n][1]) << endl;
}
int main()
{
    f[0][0] = 0;
    f[0][1] = -INF;
    int T = 1;
    cin >> T;
    while (T -- ) solve();
    return 0;
}

滚动数组优化

很多 线性DP 都可以用此类优化，详见 【01背包DP模型+朴素优化】

时间复杂度: $O(N)$

空间复杂度: $O(1)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n;
int w[N];
int f[2][2];

void solve()
{
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;

    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];
    for (int i = 1; i <= n; ++ i)
    {
        f[i & 1][0] = max(f[(i - 1) & 1][1], f[(i - 1) & 1][0]);
        f[i & 1][1] = f[(i - 1) & 1][0] + w[i];
    }
    cout << max(f[n & 1][0], f[n & 1][1]) << endl;
}
int main()
{
    int T = 1;
    cin >> T;
    while (T -- ) solve();
    return 0;
}