历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 10. 有依赖的背包问题【有依赖背包DP+子物品体积集合划分】原题链接困难

作者：

一只野生彩色铅笔 , 2021-06-23 20:28:16 , 所有人可见 , 阅读 7307

123

34

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

有 $N$ 件物品和一个体积为 $V$ 的背包

第 $i$ 件物品的体积为 $v_i$ ，价值为 $w_i$

每件物品有一个 父节点物品 $p_i$ ，如果想选第 $i$ 件物品，就必须选他的 父节点 $p_i$

拓扑结构 如下图所示：

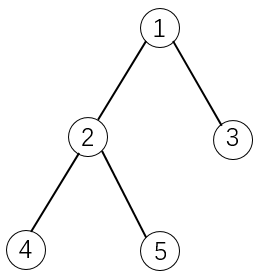
如果选择 物品5，则必须选择 物品1 和 物品2。

这是因为 物品2 是 物品5 的 父节点，物品1 是 物品2 的 父节点。

求一个方案，使得该选择的物品合法，总体积不超过 $V$ ，且总价值最大

分析

这是一道 背包DP 的 变种题目

根据题设的 拓扑结构 可以观察出每个物品的关系构成了一棵树

而以往的 背包DP 每个物品关系是 任意的（但我们一般视为 线性的）

所以，这题沿用 背包DP 的话，要从原来的 线性DP 改成 树形DP 即可

然后思考 树形DP 的 状态转移

先比较一下以往 线性背包DP 的 状态转移，第 $i$ 件物品只会依赖第 $i-1$ 件物品的状态

如果本题我们也采用该种 状态依赖关系 的话，对于节点 $i$ ，我们需要枚举他所有子节点的组合 $2^k$ 种可能

再枚举体积，最坏时间复杂度 可能会达到 $O(N\times2^N\times V)$ （所有子节点都依赖根节点）
最终毫无疑问会 TLE

因此我们需要换一种思考方式，那就是枚举每个状态 分给各个子节点 的体积

这样 时间复杂度 就是 $O(N \times V\times V)$

具体分析如下：

闫氏DP分析法

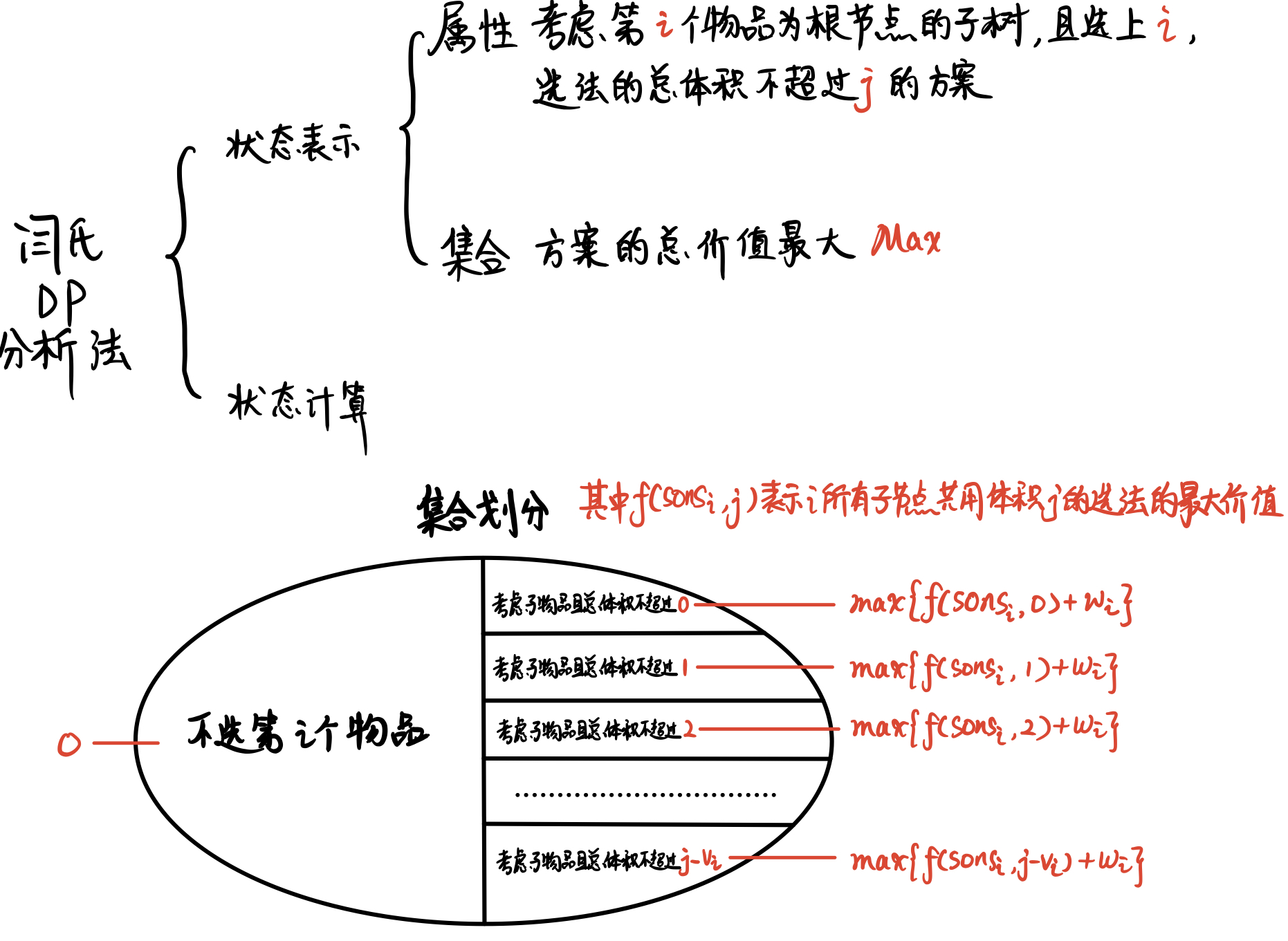
Code

时间复杂度： $O(N \times V \times V)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int n, m, root;
int h[N], e[N], ne[N], idx;
int v[N], w[N];
int f[N][N];


void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
    //先枚举所有状态体积小于等于j-v[u]的所有子节点们能够获得的最大价值
    for (int i = h[u]; ~i; i = ne[i])
    {
        int son = e[i];
        dfs(son); //从下往上算，先计算子节点的状态
        for (int j = m - v[u]; j >= 0; -- j) //枚举所有要被更新的状态
        {
            for (int k = 0; k <= j; ++ k)   //枚举该子节点在体积j下能使用的所有可能体积数
            {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    //最后选上第u件物品
    for (int j = m; j >= v[u]; -- j) f[u][j] = f[u][j - v[u]] + w[u];
    for (int j = 0; j <  v[u]; ++ j) f[u][j] = 0;   //清空没选上u的所有状态
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);
    }
    dfs(root);
    cout << f[root][m] << endl;
    return 0;
}

44 评论

福贵 2022-08-10 13:57

题解我只看铅笔哥！

浑元形意太极拳掌门人-马保国 2022-09-07 15:34

看这个字，应该是铅笔姐

wh2011 2023-08-23 10:22 回复了浑元形意太极拳掌门人-马保国的评论

铅笔是男的

Ac++Wing 2023-08-29 15:16 回复了浑元形意太极拳掌门人-马保国的评论

我一个男的字都被老师认成女的

残阳如血 2024-02-18 14:51 回复了 Ac++Wing 的评论

醒了不起的盖兹比 2023-04-25 22:25

励志走遍每一个铅笔哥的tijie

雨泉清音 2021-11-13 08:26

请问dfs中为什么这里要倒序枚举啊？for (int j = m - v[u]; j >= 0; – j)

电次君一起逃跑吧 2021-11-13 16:16

调用的上一层的倒序枚举确保这一层的只被更新一次。

正能量的阿龙 2022-06-24 15:26

分组背包就是这样

Shinytale 2023-03-25 17:53 回复了电次君一起逃跑吧的评论

但这个难道不是用的这一层的吗

Shinytale 2023-03-25 17:54 回复了电次君一起逃跑吧的评论

用的不是f[u][j-k]吗

污秽之翼 2023-10-18 16:41

保证只加一次 w[u]，因为后面的数据要依赖前面的数据

小明_68 4个月前

三年了，还是要强答一发：
这个循环是在处理某一棵子树的各种选法，而非对各个子树的枚举，大佬肯定是没注意外重的循环（我也是）

德布罗意の猫 2023-01-09 17:19

orz
大佬的题解真的太清晰了！！！！！%%%%%%%

谛 3个月前

铅笔哥，这道题目给父节点预留空间的方式为什么不可以参考”树状DP“的二叉苹果树那道题目啊，
我把你dfs函数按二叉苹果树预留父节点的方式改成了这样

void dfs(int u)
{
    //先枚举所有状态体积小于等于j-v[u]的所有子节点们能够获得的最大价值
    for (int i = h[u]; ~i; i = ne[i])
    {
        int son = e[i];
        dfs(son); //从下往上算，先计算子节点的状态
        for (int j = m ; j >= 0; -- j) //枚举所有要被更新的状态
        {
            for (int k = 0; k <= j-v[u]; ++ k)   //枚举该子节点在体积j下能使用的所有可能体积数
            {
                f[u][j] = max(f[u][j], f[u][j - k-v[u]] + f[son][k]+w[u]);
            }
        }
    }

}

然后就wa了

xiehy 7个月前

好文tql

残阳如血 2024-02-18 14:53

照片里的“属性”和“集合”是不是写反了？

VVOVV 2023-05-08 07:49

为什么是2^k的选法啊

cai_xing 2023-09-17 18:06

每种物体有两种选法，有k个物体

xianyelei 1个月前

大佬%%%%%%

厄斐琉斯 3个月前

分组背包的二维形式不是j要正序吗？这个怎么是倒序

齐山风 1个月前

因为他省掉了一维，真正完整的写法是这样

#pragma GCC optimize("Ofast","inline","unroll-loops","no-stack-protector")
#include <bits/stdc++.h>
#define MountainRain main
//#define int long long
//#define double long double
#define INF 0x3f3f3f3f
#define endl '\n'
#define fi first
#define se second
using namespace std;typedef pair<int,int> PII;typedef long long LL;typedef unsigned long long ULL;int in(){int x=0,y=0;char c=0;while(!isdigit(c))y|=c=='-',c=getchar();while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();return y?-x:x;}void out(int x){if(x<0)putchar('-'),x=-x;if(x>9)out(x/10);putchar(x%10+'0');}
const int N=110;
int n,m;
int v[N],w[N];
int h[N],e[N],ne[N],idx;
int f[N][N][N],cnt[N];
//f[u][s][j]:处理u节点的前s个子节点,体积不超过j的最大价值
//f[u][s][j]=max(f[u][s-1][j],f[u][s-1][j-k]+f[son][cnt[son]][k])
//cnt[]表示每个节点的子节点数量
void add(int a,int b)
{
    e[idx]=b;ne[idx]=h[a];h[a]=idx++;cnt[a]++;
}
void dfs(int u)
{
    // // 初始化处理0个子节点的情况
    // for(int s=0;s<=cnt[u];++s)
    //  for(int j=0;j<=m;++j)
    //      f[u][s][j]=0;
    for(int j=v[u];j<=m;++j)f[u][0][j]=w[u];
    //s表示当前正在处理的节点
    for(int i=h[u],s=1;~i;i=ne[i],++s)
    {
        int son=e[i];dfs(son);
        //需要额外考虑一点,根节点u是已经放进来了,j必须>=v[u],预留下来放u的体积
        for(int j=v[u];j<=m;++j)
        {
            //不选当前子节点,继承之前状态
            f[u][s][j]=max(f[u][s][j],f[u][s-1][j]);
            //分配k体积给当前子节点
            for(int k=0;k<=j-v[u];++k)
                f[u][s][j]=max(f[u][s][j],f[u][s-1][j-k]+f[son][cnt[son]][k]);
        }
    }
}
void solve()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    int root;
    for(int i=1;i<=n;++i)
    {
        int p;cin>>v[i]>>w[i]>>p;
        if(p==-1)root=i;
        else add(p,i);
    }
    dfs(root);
    cout<<f[root][cnt[root]][m]<<endl;
}
signed MountainRain()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cout.setf(ios::fixed),cout.precision(2);
    int T=1;//cin>>T;
    while(T--)solve();
    return 0;
}

团子团子 10个月前

j循环的倒序是由于省去了子树这一维，f[u][j-k]是不考虑本子树，考虑前面所有son，体积达到j-k的情况，类比于01背包的优化一维

baikun 2024-03-01 12:55

树形dp和分组背包的结合

污秽之翼 2023-10-18 16:26

%%% or2

hblovo 2023-07-13 10:33

for (int j = m; j >= v[u]; – j) f[u][j] = f[u][j - v[u]] + w[u];
for (int j = 0; j < v[u]; ++ j) f[u][j] = 0; //清空没选上u的所有状态
这里的思路不是很懂

早晚会 2023-08-24 07:27

兄弟你懂了吗我也不是懂

mml 25天前 ·河北回复了早晚会的评论

对每一个子树都有选择和不选择啊，因为f是从叶子到根一点一点递归加起来的，所以子树根对应的f是局部最大的，空间足够的话是一定选的。而空间不够放这个子树的根的话，那这个u点往下这个小子树全不能要了，装不进去了。（放不进去u，u往下的点都是依赖u的）

joykiller 2023-06-27 19:27

这个字也太好看了%%%%%

小白熊要学算法 2023-04-09 10:13

’‘’void dfs(int u)
{
for(int i=h[u];i != -1;i = ne[i])
{
int son= e[i];//遍历主件
dfs(son);
for(int j=v[u];j<=m;j)
{
for(int k=0;k<=j-v[u];k)
{
dp[u][j] = max(dp[u][j],dp[u][j-k]+dp[son][k]);
}
}

}
for(int i=m;i>=v[u];i--) dp[u][i] = dp[u][i] + w[u];
//for(int i=1;i<v[u];i++) dp[u][i] = 0;

}’‘’
我就只改动了最后枚举体积和物品的情况，请问是哪里不对呀233

oy9r 2023-01-18 10:31

以为是二叉树

AC不了怎么办 2022-07-04 21:11

请问最后选上第u件物品,为啥要从大到小枚举呢?

wuxiangzhuansheng 2022-08-03 18:10

因为要用小的来更新大的，不能用已经更新的去更新别的

谜之阴雨 2022-05-09 17:11

e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; 有大佬能说一下这里e[idx] ，ne[idx]，h[a]，idx分别是什么吗

锦木千束 2022-05-19 14:52

我的理解是e数组存储的是节点的值，ne存储的是当前节点的下一个节点，h存储的是头节点的位置，idx简单理解成指针

huwqchn 2022-06-04 15:32

数组的本质其实是个映射,
h数组的映射是点的编号 -> 最新添加的出边的编号的映射（因为是头插法），
e数组的映射关系是，入边的编号 -> 这条边指向的点的编号的映射，
ne数组是，边 -> 下一个同样起点的边的映射，
idx表示边的编号，每次用一条就++，保证所有边的编号不一样，最后idx就代码这张图有多少条边。

mml 25天前 ·河北

建议先搜搜邻接表的结构图啥样再对应这个代码看

seth 2021-12-19 22:42

图的集合和属性写反了233

App 内打开

AcWing 10. 有依赖的背包问题【有依赖背包DP+子物品体积集合划分】 原题链接 困难

题目描述

分析

闫氏DP分析法

Code

44 评论

AcWing 10. 有依赖的背包问题【有依赖背包DP+子物品体积集合划分】原题链接困难