最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

金明今天开心了，你呢😂

一共有 $N$ 元钱，$M$ 件 物品

每件 物品 价格 是 $v_i$ 元，权重 是 $w_i$，价值 是 $v_i \times w_i$

求一种方案，使得购买的 总价值 最大

分析

这是一道 01背包 的裸题

只是 物品 的 价值 的计算需要额外用到文中给出的公式 $v_i \times w_i$

其他基本一致，我就水一篇题解啦

下面都是照搬的原文 AcWing 423. 采药【01背包DP模型+朴素优化】

01背包模型

状态表示$f(i,j)$—集合： 考虑前 i 个物品，且当前已使用体积为 j 的方案

状态表示$f(i,j)$—属性： 该方案的价值为最大值 $\max$

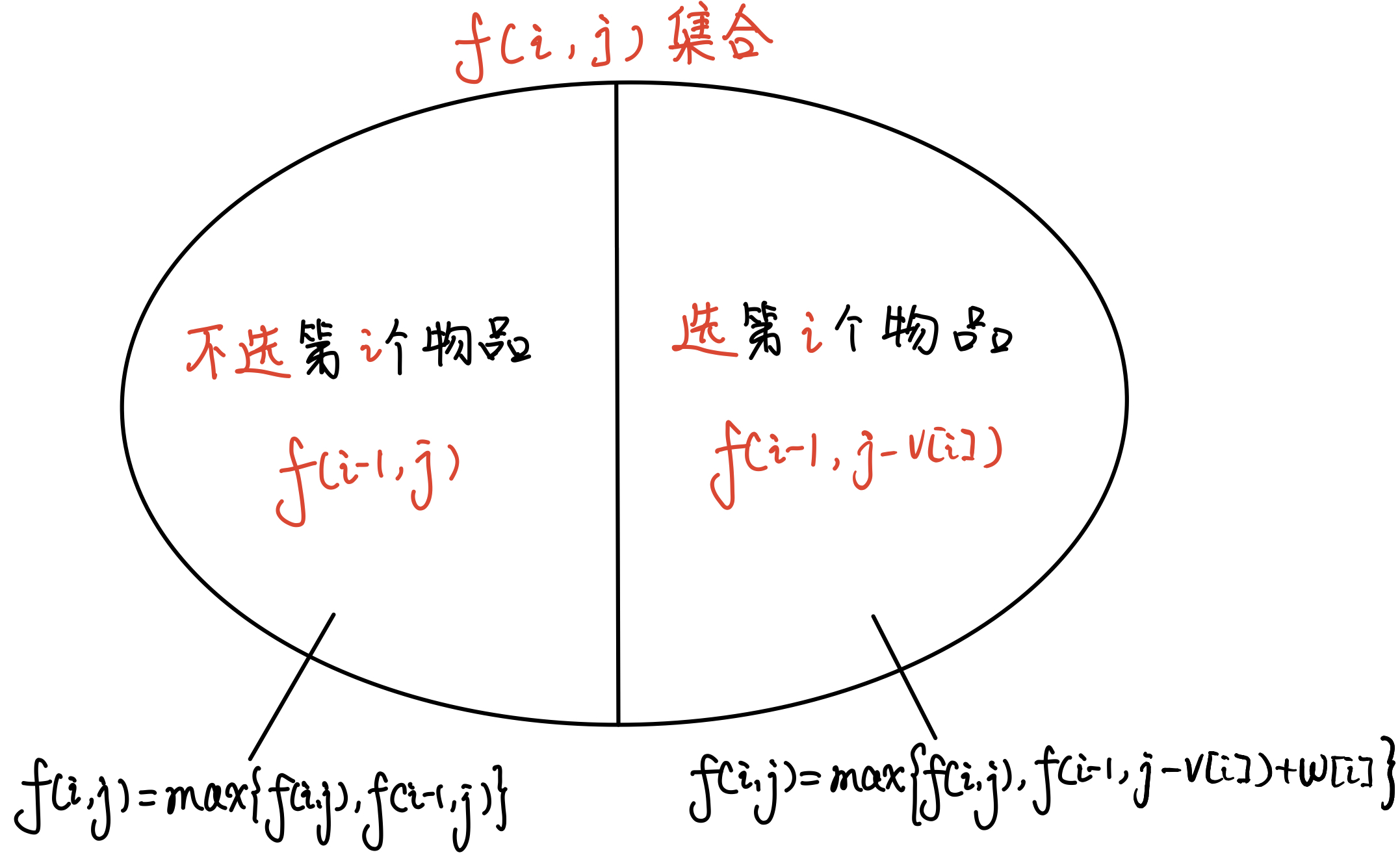
状态转移$f(i,j)$： $f(i,j) = \begin{cases} 不选第i个物品： &\max\{f(i-1,j)\} \\\ 选第i个物品：&\max\{f(i-1,j - v_i) + w_i\} \end{cases}$

初始状态：f[0][0]
目标状态：f[n][m]

集合划分

Code

时间复杂度：$O(n \times m)$

#include <iostream>

using namespace std;

const int N = 30, M = 30010;

int n, m;
int v[N], w[N];
int f[M];

int main()
{
    cin >> m >> n;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i], w[i] *= v[i];
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = m; j >= v[i]; -- j)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}