题目描述

给定一个N行N列的棋盘，已知某些格子禁止放置
求最多能往棋盘上放多少块的长度为2、宽度为1的骨牌，骨牌的边界与格线重合（骨牌占用两个格子），并且任意两张骨牌都不重叠。

输入样例：

8 0

输出样例：

32

解决方案
匈牙利算法 时间复杂度O(n^4)

这里时间复杂度的分析就是假设一次遍历要遍历所有的边，白能力n^2次，一次遍历n^2条边，故时间复杂度为O(n^4)

首先我们知道，使用匈牙利算法的前提是这张图是一个二分图，这里对于一张棋盘，如下

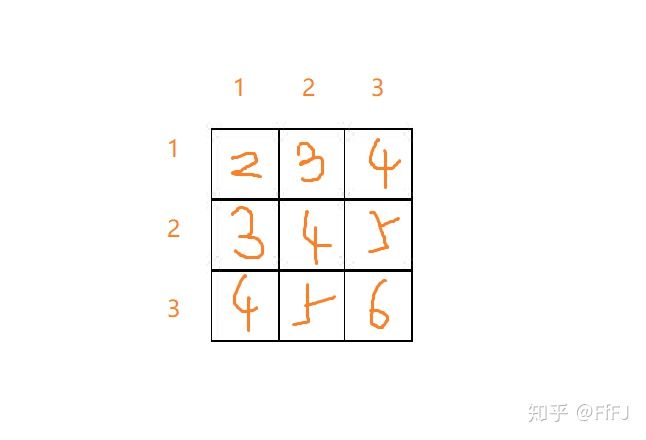
这里我们以i+j的值为图中每个方块的标记，将所有的偶数染成白色，所有奇数染成黑色（对棋盘进行二染色），最后我们可以发现，每一个方块的四周，都不会有和它一样颜色的方块，也就是一个骨牌不可能覆盖相同颜色的两个点(同一集合中不会有边)，那我们将值为偶数的方块放到一个集合中，值为奇数的方块放到一个集合中，构造一个二分图，把题目中的骨牌看作连接两个方块的一条边，不让骨牌重叠就是不让两条边有重叠的点，放最多的骨牌就可以看作找到最多的边，分析到这里，我们发现，这其实就是一个二分图的最大匹配问题，也就是匈牙利算法，问题就迎刃而解了！！

Java：

import java.io.*;
import java.util.*;

class Main{
    static int N=110,M=2*N;

    static boolean[] g=new boolean[N*N];
    static boolean[] s=new boolean[N*N];
    static int[] match=new int[N*N];

    static int[] h=new int[N*N];
    static int[] e=new int[M*M];
    static int[] ne=new int[M*M];
    static int idx;
    static int[][]mv= {{1,0},{-1,0},{0,1},{0,-1}};

    static void add(int a,int b){
        e[idx]=b;
        ne[idx]=h[a];
        h[a]=idx++;
    }

    static boolean find(int cur){
        for(int i=h[cur];i!=-1;i=ne[i]){
            int j=e[i];
            if(s[j]) continue;
            s[j]=true;
            if(match[j]==0||find(match[j])){
                match[j]=cur;
                return true;
            }
        }

        return false;
    }

    public static void main(String[]args)throws IOException{
        Arrays.fill(h,-1);
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        String[]arr=in.readLine().split(" ");
        int n=Integer.parseInt(arr[0]);
        int m=Integer.parseInt(arr[1]);

        while(m-->0){
            String[]num=in.readLine().split(" ");
            int a=Integer.parseInt(num[0]);
            int b=Integer.parseInt(num[1]);
            int c=(a-1)*n+b;

            g[c]=true;
        }

        //加边
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                int cur=(i-1)*n+j;
                if(g[cur]) continue;//如果这个点不能放置骨牌，就直接跳过
                if((i+j)%2==0) {//只给偶节点加边
                    for(int k=0;k<4;k++){
                        int nx=i+mv[k][0];
                        int ny=j+mv[k][1];
                        if(nx<1||nx>n||ny<1||ny>n) continue;
                        int now=(nx-1)*n+ny;
                        if(g[now]) continue;
                        add(cur,now);
                    }
                }
            }
        }


        int res=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if((i+j)%2==0) {
                    int cur=(i-1)*n+j;
                    if(g[cur]) continue;//如果这个点不能防止骨牌，就直接跳过
                    Arrays.fill(s,false);
                    if(find(cur)){
                        res++;
                    }
                }
            }
        }

        System.out.println(res);
    }
}

C++：

#include <iostream>
#include <algorithm>
#include <cstring>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N=110;

int n,m;
bool g[N][N],st[N][N];
PII match[N][N];

int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};

static bool find(int i,int j)
{
    for(int k=0;k<4;k++)
    {
        int a=i+dx[k],b=j+dy[k];
        if(a<1||a>n||b<1||b>n) continue;
        if(st[a][b]||g[a][b]) continue;
        st[a][b]=true;

        PII t=match[a][b];//找到当前的这个节点匹配的点
        if(t.x==0||find(t.x,t.y))
        {
            match[a][b]={i,j};
            return true;
        }
    }

    return false;
}

int main()
{
    cin>>n>>m;

    //将所有的坏格子标记为true
    while(m--)
    {
        int x,y;
        cin>>x>>y;

        g[x][y]=true;
    }

    int res=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(g[i][j]) continue;
            if((i+j)%2==0)
            {//为奇点找匹配的偶点
                memset(st,0,sizeof st);
                if(find(i,j)) res++;
            }
        }
    }

    cout<<res<<endl;

    return 0;
}